Infectious Chocolate Joy with a Side of Poissonian Statistics: An activity connecting life science students with subtle physics concepts
Published online:
Abstract
Introductory physics courses are required for many programs in the life sciences, yet traditional curricula fail to help students meaningfully connect physical concepts with biological systems. In this lesson, we describe an activity taught in a large introductory physics class designed for life science majors (n = 143; 80% premedical students). The lesson was integrated in a novel curriculum focusing on a quantitative approach to biological topics. Students often hold the misconception that biological processes always happen in a uniform manner. This activity uses the biological example of a human immunodeficiency virus (HIV) infecting T lymphocytes (T cells) to motivate understanding of the macroscopic distribution of HIV in T cells, a non-uniform, Poisson distribution. In the spirit of scientific teaching and scientific inquiry, the lesson begins with students making a prediction and then testing it with a deceptively simple hands-on simulation that uses chocolate candy as a proxy for HIV and plastic Easter eggs to play the role of T cells. The lesson requires groups of students to collect, analyze, and interpret data from this simulation. Students then enter into an open-ended discussion on the validity of modeling different events as a Poisson distribution. Our observations and student feedback indicate that this lesson stood out as one of the most engaging and memorable activities during the semester. Students were able to recognize and apply the definition of a Poisson distribution to given examples as well as in future assignments and exams.
Citation
Holland, E.T., Manley, G., Chiba, T., Ramos, R., Mochrie, S. and Frederick, J. 2015. Infectious Chocolate Joy with a Side of Poissonian Statistics: An activity connecting life science students with subtle physics concepts. CourseSource. https://doi.org/10.24918/cs.2015.9Society Learning Goals
Bioinformatics
- Computation in the life sciences
- What is the role of computation in hypothesis-driven discovery processes within the life sciences?
Science Process Skills
- Process of Science
- Pose testable questions and hypotheses to address gaps in knowledge
- Plan, evaluate, and implement scientific investigations
- Interpret, evaluate, and draw conclusions from data
- Construct explanations and make evidence-based arguments about the natural world
- Address novel questions through authentic research experiences
- Modeling/ Developing and Using Models
- Recognize the important roles that scientific models, of many different types (conceptual, mathematical, physical, etc.), play in predicting and communicating biological phenomena
- Make inferences and solve problems using models and simulations
- Build and evaluate models of biological systems
- Quantitative Reasoning/ Using Mathematics and Computational Thinking
- Apply the tools of graphing, statistics, and data science to analyze biological data
- Communication and Collaboration
- Share ideas, data, and findings with others clearly and accurately
Lesson Learning Goals
- Students will understand what it means for biological processes to be Poissonian.
- Students will appreciate the relationship between the average occurrence of an event and the probability of the event occurring.
- Students will carry out the process of scientific inquiry.
Lesson Learning Objectives
- Students will define a Poisson distribution.
- Students will generate a data set on the probability of a T cell being infected with a virus(es).
- Students will predict the likelihood of one observing the mean value of viruses occurring.
- Students will evaluate the outcomes of a random process.
- Students will hypothesize whether a process is Poissonian and design a test for that hypothesis.
- Students will collect data and create a histogram from their data.
Article Context
Course
Article Type
Course Level
Bloom's Cognitive Level
Vision and Change Core Competencies
Vision and Change Core Concepts
Class Type
Class Size
Audience
Lesson Length
Pedagogical Approaches
Principles of How People Learn
INTRODUCTION
In fall 2013, Yale University’s introductory physics course for life scientists (PHYS170) was completely redesigned to incorporate evidence-based approaches of ‘scientific teaching’ (1). PHYS170, unique in its own right, was conceived by Professor Simon Mochrie (2) to better align with the interests of our students (3-5) and to incorporate the excitement of modern research by meaningfully linking physical concepts and biological processes in what is typically the last physics course for a life scientist (6,7). In this lesson, we present a 25 minute, in-class activity used to improve students’ conceptual grasp of a Poisson distribution in a biological context. The Poisson distribution is typically introduced in a sophomore level physics class, out of tradition, as “the law of rare events” and is accompanied by the anecdote of Ladislaus Bortkiewicz using the Poisson distribution to investigate the number of soldier deaths due to horse kicks in the Prussian army (8). Although memorable, this example does not help students develop an innate conceptual understanding of the probability distribution. In fact, associating the Poisson distribution only with rare events is misleading for it can be used to model frequent events as well. Classroom activities of Poissonian statistics exist for physics classes and laboratories; however, these typically involve x-ray tubes, Geiger counters, or use household materials for abstract applications (9-11). In the spirit of using an authentically biological example, we developed this in-class activity demonstrating that the Poisson distribution need not model rare events and is applicable to biological processes. This activity complements an example of the Poisson distribution found in the textbook—the occurrences of breast cancer in women.
The majority of PHYS170 students were sophomores or juniors, with seniors comprising the remainder of the class. Sixty-four percent of the 2013 class self-identified as biology majors and eighty percent of the class was on a pre-medical track. Due to the life science curricula at Yale University, students in PHYS170 are guaranteed to have taken at least one full year of introductory biology. Furthermore, approximately eighty-four percent have previously taken a physics course in high school. Although this activity was completed in an introductory physics course, its focus on reasoning and the scientific method renders the activity appropriate for other courses, including a course in quantitative biology or for non-science majors. Although not essential, prior exposure to the biological concept of viral infection would be an advantage for students. If students are unfamiliar with viral infection, the instructor may wish to give a 5 minute lecture about HIV, T-cells, and how HIV infects T-cells.
SCIENTIFIC TEACHING THEMES
Active Learning
This activity draws on the fundamentals of scientific teaching by engaging students, incorporating formative and summative assessment, and fostering inclusiveness. Students are required to work in teams, use physical models, generate and analyze data, and make predictions in this activity.
Assessment
The pre-activity is a self-assessment for students to review basic probability calculations and the definition of a Poisson distribution. Students rely on this foundation during the activity to make a prediction and collect data. Interaction between students and the instructor provide the basis for frequent formative assessment during the activity. In several instances, students discuss and expand their knowledge by leveraging peer teaching to arrive at the correct answer as a group. Through the data analysis portion, students demonstrate their ability to explain and compare their results in the context of a Poisson distribution (Figure 1). For a summative assessment, we created a worksheet (Supplemental File S1) where students record their group work and answers to the discussion questions.
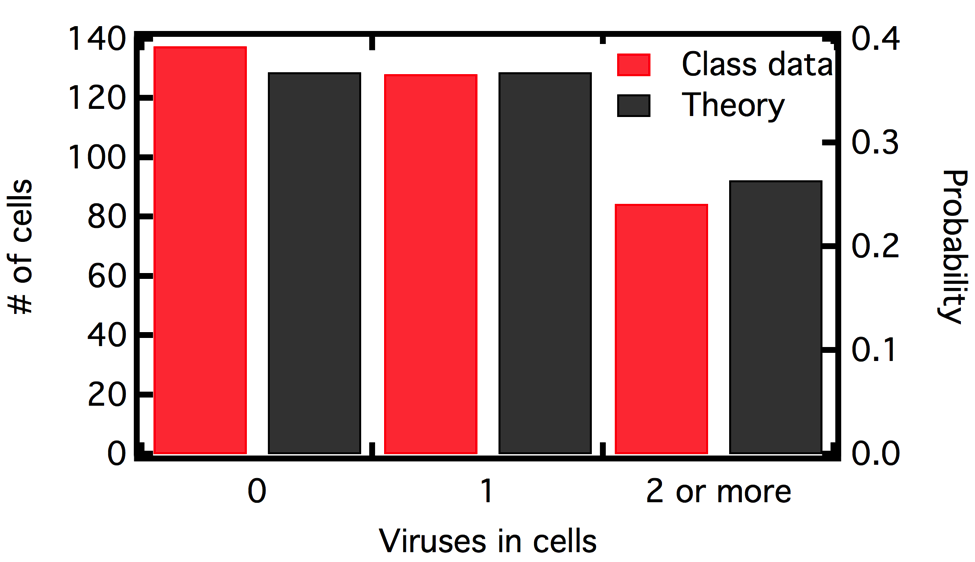
Figure 1. Class results from the simulation (red) which are compared to a Poisson distribution (black) each of which have an average infection of one virus per cell. From the above, students should be convinced that having exactly one infection in a cell is not the most likely event. Furthermore, students should also see that a Poisson distribution matches the simulated outcome quite well. Any discrepancies are due to numerical fluctuations.
Inclusive Teaching
By design, this activity is meant to include and encourage students to learn in an intellectually safe environment. At the beginning of the lesson, students make a prediction about the likelihood of an uninfected T cell occurring in a population that contains equal numbers of HIV particles and T cells. Making a prediction increases students’ curiosity and intellectual investment in the activity (12,13). The core of the activity is creating a simulation by passing a mock petri dish around as they ‘infect’ plastic eggs. By default, friendly attention was drawn to the person holding the petri dish. The opening, inserting, closing, and mixing parts offer students a kinesthetic feel so that later they may associate this process with this distribution. Because every student participates, this inclusion helps shy students voice their opinions when it is their turn to contribute. We note that this activity used Easter eggs for convenience and economy. Instructors will need to be sensitive about the association of Easter eggs with a Christian holiday, and that a religious reference may exclude some students. Alternatives to Easter eggs include plastic food bags, sewing kits, ring boxes, or change purses. We found no evidence that our students connected the use of Easter eggs to promotion of a Christian holiday. In our class, students reacted positively to the brightly colored eggs and the opportunity to eat leftover candy.
LESSON PLAN
Classroom Context: This activity was taught in an active learning classroom outfitted with fourteen tables that each seated roughly ten students. To implement this activity in a traditional lecture hall, the instructor could use rows of students as a proxy for tables, with students at the end of a row passing the plastic bag back in the direction from which it came.
The core of this activity is the hands-on simulation of a viral infection. Students pass around a bag of plastic (Easter) eggs that are drawn at random, ‘infected’ with a piece of chocolate, and returned to the bag so that a given plastic egg has a chance of being drawn again and ‘re-infected’ with additional pieces of chocolate. We intend that the activity is ‘minds-on, hands-on’ so that students build a kinesthetic connection to link the mathematical distribution and HIV infection of T cells. For each table, we provided twenty Easter eggs (representing T cells) and twenty Hershey chocolate kisses (representing HIV particles) in a plastic shopping bag (representing a petri dish). To simulate larger multiplicities of infection, one could use different colored chocolate pieces to represent one, three, five, or ten viruses (Table 1 and Table 2).
Tables 1 and 2. Infectious Chocolate Joy
Pre-class Teacher Preparation: The Easter eggs were purchased on Amazon for convenience, price, and quantity. With some foresight the plastic eggs could be purchased during the appropriate season without much trouble. Before class, plastic shopping bags were filled with twenty Easter eggs and an equal number of Hershey kisses. These bags were not distributed to the class until we began the activity so as not to distract students. For hygiene purposes we preferred to use individually wrapped candy pieces rather than M&Ms or other unwrapped candy.
Pre-class Student Preparation: Students are asked to read the first page of the Poisson distribution worksheet (Supplemental File S1) and are required to submit feedback (Supplemental File S2) on their reading through the channel of the instructor’s choice. To accomplish this, we used LearningCatalytics, a web-based response system similar to clickers. In the future, we will be using our university based class website due to its simplicity and innate linkage with the online grade book. The pre-class activity introduces students to the idea of a Poisson distribution and engages students by soliciting their thoughts and feedback about the introductory materials. We suggest including an open-ended question asking students to report what they found confusing in the homework and what they would like to have clarified. Our activity largely addressed student pre-class questions and we incorporated any points of confusion as fodder for inspiring any lagging conversation.
In-class Part 1: Students Make a Prediction. (2 minutes)
“Working in groups, please predict the likelihood of having a null event, exactly one event, or two or more events in the Poisson distribution. Once you have completed this please work on the design question for this activity.”
Students refer to the handout for the formula for a Poisson distribution and use that formula to calculate the probability of obtaining zero, one, or more than one virus infection per cell, assuming a Poisson distribution with an average infection of one virus per cell. Students have two minutes to complete this part (Table 1). An interesting observation students may discover is that having an uninfected cell or a cell with only one infection are equally likely events in the case of an average infection of one virus per cell. Once their calculations are complete, students predict how many uninfected T cells would be present if there were an equal number of HIV and T cells.
In-class Part 2: HIV Infection Simulation (10 minutes)
“We will now carry out a simulation of an equal number of viruses, which will be represented as chocolate pieces, and t-cells, which will be represented as Easter eggs. Each table should have a bag with an equal number of Easter eggs and candy but before you begin verify that this is indeed the case. If everything is in order, then carefully read the directions and begin the activity. Remember to discuss with your group while you complete this activity. Once you have completed this part of the activity please let an instructor know. Have fun!”
Much to our surprise and delight this part of the activity went quite smoothly. Students were focused, no computers or cell phones out, and collaborative sharing of ideas in a group setting occurred. As students followed the worksheet, they discussed the reasoning behind the steps of activity to encourage a connection between the simulation physical concepts (Supplemental File S1).
In-class Part 3: Interpreting the Simulation Results (5 Minutes)
“Now that all your candy is in the Easter eggs, your group needs to determine how many times an egg has zero candy, one, or more than one. Have one or two people record the results as the group determines this. Please submit your answers to the Google survey that has been shared with you.”
Student are given five minutes to decide how to quantify the results of their simulation (Table 1). Students are reminded to be diligent and write down their observations as they complete this analysis, for the worksheets will be collected at the end of class. Since students cannot see inside the eggs, they must eventually decide that they have to open the eggs and record the number of chocolates in each one. We recommend circulating among the tables to discuss plans for recording data before giving students the “green light” to begin opening eggs. The best method is to have students create a histogram for these events (Figure 1). Specifically, students should record the number of eggs that contain no candy, one piece, and two or more pieces. Students enter their table’s information into a shared Google survey, but students could make their own spreadsheets or use another graphing program. Students then convert the histogram to a measured probability distribution by dividing the number of times a given outcome occurred by the total number of kisses.
In-class Part 4: Would you, could you model another scenario as a Poisson distribution? (5 minutes?)
The activity concludes with a variety of different scenarios that extend the activity beyond the scope of viral infection. Students must discuss, decide, and defend whether or not it is appropriate to model the events in the worksheet scenario as a Poisson distribution. Two scenarios that spurred a lot of discussion were whether the arrival of emails in your inbox or the number goals scored in a soccer match could be modeled as a Poisson distribution.
Post-class: Each student turns in the completed worksheet from the activity. We had students turn in their worksheet with their homework and graded for completeness.
TEACHING DISCUSSION
Before fall 2013, PHYS170 was taught as a traditional lecture course. Since fall 2013, PHYS170 has been taught in the technology enabled active learning (TEAL) classroom as a nontraditional lecture course, with students’ expectations of what a physics course will entail no longer valid. As a result, students expressed resistance to active learning throughout the semester and into PHYS171, the second course in the year-long physics sequence. We suspect that students’ lack of experience with peer instruction and with other interactive learning methods were factors in student resistance to active learning. It was with great relief that we noticed that, in contrast to their behavior during other activities, students were focused, self-organized, and eagerly discussing the HIV infection activity. Since this activity was taught halfway through the semester, it was rewarding to observe students finally buying into active learning, as evidenced by students’ enthusiasm, positive attitudes, as well as their lively discussion, which normally did not occur. In fact, this activity was among the most enjoyed by both the students and the instructors. We suspect that having clearly stated learning goals aligned with the activity helped students realize how the activity was helping them learn the material. During the activity, students typically excelled on lower level Bloom’s taxonomy questions requiring memory recall or applying definitions, as evidenced by students completing the memory recall sections correctly and in a timely manner. For higher-level Bloom’s taxonomy skills, students as a whole performed reasonably well, based on the instructors’ discussions with students and discussions overheard amongst students. In general, students enjoyed that this straightforward in-class activity led to a surprising, counterintuitive result. Furthermore, students relished the opportunity to discuss their predictions on different scenarios. Answers students submitted to discussion questions for this activity help support this claim that students were gaining science process skills. For instance, students not only described whether or not a scenario could be a Poisson distribution but also addressed short comings of that approximation and commented on whether or not they felt it would be a significant impact. In the future, we intend to ask more experimental design questions to evaluate whether students who completed this activity achieved gains in scientific process skills during the semester.
The discussion portion at the end of the lesson opened with Professor Mochrie describing the debate he had with a teaching fellow before class about whether or not one could model the arrival of emails in one’s inbox as Poissonian. He claimed that, since his emails are largely independent of one another, a Poisson model would be suitable. Since the teaching fellow uses her email for ongoing conversation threads with friends, her inbox would not fit a Poisson distribution because her emails are not independent. In retrospect, showing that two authority figures can disagree with good reasons and both be correct was entertaining and edifying. The friendly debate put students at ease and led to the liveliest discussion of the semester. We intend to keep the spirit of this impromptu debate by developing a skit where authoritative figures take opposing sides that can both be justified as correct.
The strong points of this activity are that it is relatively inexpensive and it is statistically valid, as long as students mix the bag to ensure randomization (and do not snack on the chocolate until the end of the activity). Chocolate candy is the biggest expense, which could be avoided by using less expensive candy, pebbles, or even cardboard “viruses.” A common obstacle to implementing active learning exercises is concern that the activity will not function and that class time will be wasted solving technical issues. This activity overcomes that challenge by requiring no technical equipment with the potential of not working. In addition, even if students are not diligent in their random selection process, it still “works.” For example, if students only grab the few eggs on top without mixing, then just a few eggs will have all the candy. The results will not align with a Poisson distribution, but they will demonstrate the point that an average of one infection per cell does not mean every cell has an infection. Thus, the pedagogical value of this activity is preserved even if students don’t follow directions carefully.
This activity could be readily implemented without modification in smaller classes or by teaching assistants in the discussion sections of large classes. Larger, stadium-style classrooms will require more planning and hands-on help. Even in our TEAL classroom, support from teaching assistants familiar with the activity contributed to its success. For a large lecture class with traditional stadium style seating, the activity could be implemented using rows as groups and having students pass the bag back and forth along a row. If possible, blocking off every third row so instructors may walk through and check in with students could help configure a large lecture hall to work more effectively for the activity.
Because we did not secure release forms for photographs during the fall 2013 class, we staged a photo for this activity in April 2014. Two of the students in the photograph had completed the lecture-based version of PHYS170 and were quite curious when a bowl full of Easter eggs was placed on the table. Much to our delight, the other students who had taken the interactive version of PHYS170 began explaining all the subtleties of this activity. After they were finished explaining why even with an average value of one, the majority of cells would not contain exactly one virus, all the students quietly reflected. One student admitted, “I don’t remember what we needed to memorize.” We assured the student that she knew all she needed to and that her explanation was more than sufficient to prove mastery of the subject.
In future implementations we envision including a summative assessment to evaluate students’ ability to design experiments. For instance, we could ask: if one wanted to run an experiment in the lab and ensure that more than 95% of cells were infected with HIV, what would the average number of infections per cell be? (The answer is three or more infections.)
SUPPLEMENTAL MATERIALS
- Table 1. Infectious Chocolate Joy-Materials cost
- Table 2. Infectious Chocolate Joy-Teaching Timeline
- Figure 1. Infectious Chocolate Joy-Class results from the simulation which are compared to a Poisson distribution
- Supplemental File S1. Infectious Chocolate Joy-Poisson Distribution Worksheet
- Supplemental File S2. Infectious Chocolate Joy-Poisson Distribution Worksheet Solutions
ACKNOWLEDGEMENTS
We would like to acknowledge and thank the PHYS170 teaching fellows from fall 2013: Claudia De Grandi, Elizabeth Boulton, Shany Danieli, Brooke Russell, Jared Roveny, Raphael Safarti and Stefan Elrington. We would like to thank Helena Gali, Danielle Temares, Cora Ormseth, Katie Underwood, Layla Khuri, Christian Maxwell, Michael Cruciger, and Chris Tokita for posing for our picture. In addition we would like to thank feedback we have received from the spring 2013 Yale Scientific Teaching class. We would also like to thank Matt Reagor for insightful discussion and feedback during the development of this activity and this manuscript. Finally, we would like to thank the PHYS170 students for their enthusiasm during this activity and their feedback afterwards.
References
- Handelsman J, Miller S, Pfund C. 2007. Scientific Teaching. New York, NY:W.H. Freeman.
- Mochrie, S.G. J. 2011. The Boltzmann Factor, DNA melting, and Brownian ratchets: Topics in an introductory physics sequence for biology and premedical students. Am. J. Phys. 79(11):1121-1126.
- Association of American Medical Colleges and the Howard Hughes Medical Institute, “Scientific foundations for future physicians,” 2009, 〈http://www.hhmi.org/news/aamc-hhmi-committee-defines-scientific-competencies-future-physicians〉.
- National Research Council, BIO2010: Transforming Undergraduate Education for Future Research Biologists (National Academies Press, Washington, DC, 2003), 〈www.nap.edu/openbook.php?isbn=0309085357〉.
- American Association for the Advancement of Science, Vision and change in undergraduate biology education: A call to action (AAAS Press, 2011).
- J. Rigden, in The Changing Role of Physics Department in Modern Universities, E. F. Redish, J. S. Rigden, eds., AIP Conf. Proc. 399, American Institute of Physics, Woodbury, New York (1997), vol. 1, p. 133.
- R. C. Hilborn, Am. J. Phys. 65, 175 (1997).
- L. von Bortkiewicz. Das Gesetz der kleinen Zahlen. BG Teubner, 1898.
- M. S. Lafleur, P. F. Hinrichsen, P. C. Landry and R. B. Moore. The Poisson distribution: An experimental approach to teaching statistics. Physics Teacher, 10(6):314–321, 1972.
- W. T. Vetterling. Demonstrating Poisson statistics. American Journal of Physics, 48(5):342–344, 1980.
- P. Hinrichsen. The Poisson and interval distributions. American Journal of Physics, 42(3):231–238, 1974.
- C. Crouch, A. P. Fagen, J. P. Callan, and E. Mazur. Classroom demonstrations: Learning tools or entertainment? American Journal of Physics, 72(6):835–838, 2004.
- L. A. Kasmer and O.K. Kim. The nature of student predictions and learning opportunities in middle school algebra. Educational Studies in Mathematics, 79(2):175–191, 2012.
Article Files
Login to access supporting documents
Infectious Chocolate Joy with a Side of Poissonian Statistics- An activity connecting life science students with subtle(PDF | 187 KB)
Supplemental File S1. Infectious Chocolate Joy-Poisson Distribution Worksheet(PDF | 112 KB)
Supplemental File S2. Infectious Chocolate Joy-Poisson Distribution Worksheet Solutions(PDF | 175 KB)
- License terms

Comments
Comments
There are no comments on this resource.