A first lesson in mathematical modeling for biologists: Rocs
Published online:
Abstract
Using a fictitious population of Rocs, a mythical species of giant raptor, students accomplish two broad objectives: 1) they undertake the process of building a first mathematical model of a population, and 2) they begin to develop their understanding of the product of a scientific model. Students accomplish these objectives by engaging deeply with a system of linked scientific practices: developing scientific models collaboratively, to explain or predict observations, to multiple audiences using multiple representations. The lesson is scalable from large introductory biology courses to upper-division courses in population ecology or biological modeling. The scenario unfolds within as little as a single 50-minute class period and requires no prior preparation of students. During and after the class meeting, students work in collaborative teams to build a simple, but non-trivial spreadsheet model. Students then use their model to engage in several modeling-related activities: they use their model to make predictions, conduct a sensitivity analysis, make decisions, and communicate their model results to non-experts. This lesson invites both students and instructors to collaborate, as students work to master concepts of population growth, and scientific practices of modeling, working with data, communication, and collaboration.
Citation
Hoskinson, A.M. 2016. A first lesson in mathematical modeling for biologists: Rocs. CourseSource. https://doi.org/10.24918/cs.2016.14Society Learning Goals
Ecology
- Populations
- How do populations change over time?
- Interactions within Ecosystems
- How do systems change over time?
Science Process Skills
- Process of Science
- Interpret, evaluate, and draw conclusions from data
- Construct explanations and make evidence-based arguments about the natural world
- Modeling/ Developing and Using Models
- Build and evaluate models of biological systems
- Quantitative Reasoning/ Using Mathematics and Computational Thinking
- Apply the tools of graphing, statistics, and data science to analyze biological data
- Communication and Collaboration
- Share ideas, data, and findings with others clearly and accurately
Lesson Learning Goals
- Students will gain experience with the scientific practice of mathematical modeling.
- Students will understand real-world applications of scientific modeling.
- Students will grapple with uncertainty in science and in natural systems.
Lesson Learning Objectives
- Systematically develop a functioning, discrete, single-species model of an exponentially-growing or -declining population.
- Use the model to recommend appropriate action for population management.
- Communicate model output and recommendations to non-expert audiences.
- Generate a collaborative work product that most individuals could not generate on their own, given time and resource constraints.
Article Context
Course
Article Type
Course Level
Bloom's Cognitive Level
Vision and Change Core Competencies
Vision and Change Core Concepts
Class Type
Class Size
Audience
Lesson Length
Pedagogical Approaches
Principles of How People Learn
Assessment Type
INTRODUCTION
Origin of Lesson
In my first academic position after finishing my Ph.D., I developed a course in mathematical modeling for biologists (2) that emphasized students practicing modeling, just as much as reading about how scientific models in biology were developed. A single-species population model is a logical first model, because it requires no special conceptual knowledge. The first semester of the course, I had students build a model of the population of white-tailed deer (Odocoileus virginianus) in Georgia. Like the good students they were, they simply googled the life-history traits, plugged them into their spreadsheets, and got what they considered the Right Answer. I realized I needed to be able to control students' access to facts and information about the system, a goal I accomplished by using a fictitious species. Since that time, I have improved and revised this lesson based on student performance and learning.
Context and Rationale
The context for this lesson comes from a story of Rocs, a fictitious species of raptor. Rocs were enshrined in One Thousand and One Nights, a collection of Arabic folk tales. The other important piece to the rationale of this lesson is the practice of scientific modeling. A growing body of work shows that students at all levels of education benefit from engaging in practices such as modeling, argumentation, and working with data (1-3). Even very young or very inexperienced students can engage deeply in scientific practices (4, 5). In addition, people advance their thinking and learning skills when they engage in the same work as expert scientists (6). For these reasons, the scientific practice of modeling figures equally in this lesson with the biological concept of population growth.
All scientific models are functional simplifications of what are often very complex phenomena. Therefore, scientific models are defined by their objectives or functions, which usually fall under broad categories of describing, explaining, making predictions, or some combination of these. Regardless of objectives or disciplines, from physics, biology, chemistry, to earth sciences, all scientific models share certain features: [2, 7, 8]
- Scientific models incorporate facts - that is, data and information including prior knowledge.
- Because scientific models are simplifications, they all make systematic assumptions - simplifying hypotheses - about the phenomenon being modeled.
- At the heart of every scientific model is what the modelers or audience needs to know - that is, facts and information that could be important in building the model and obtaining useful output.
- Every scientific model includes at least one, but often many, representations. Depending on the model objective and audience, representations could include diagrams, equations, graphs, and especially in biology, depictions of cycles (e.g., life cycles, cycles of matter) and processes (e.g., metabolic reactions).
Scientific models also share some common features in their process of development. First, and fundamentally, most scientific models are collaborative enterprises. It takes multiple people, each with different strengths, areas of expertise, and points of view, to create a robust scientific model. All scientific models undergo validation, to ensure that the model explains or predicts the phenomenon of interest and that it accounts for all known facts or observations. Scientific models are always subject to revision and improvement as new facts and information become available. These features form a framework for the lesson itself and provide a systematic approach for students to adopt in future modeling experiences.
Students' Prior Knowledge
I discovered that students didn't make random, unpredictable mistakes in building and implementing their models, any more than they make random errors about many concepts. Most students had some exposure to exponential growth in their middle-school courses, and therefore tend to think that populations will always grow. Students also tend to think about populations abstractly, and have trouble linking the math with the biology of a system. For example, many students will report negative final population censuses or non-integer populations (i.e. fractions of individuals). Beginning modelers also want to report a Right Answer that represents some certain, guaranteed result. This lesson is specifically designed to help students with these mistakes.
Intended Audience
This lesson has been taught to students in introductory large-enrollment courses and to students in gateway and upper-division subject courses (ecology, population biology, modeling). The main differences lie in the degree of interactivity available with smaller courses and in the structure of the homework for each audience.
Required Learning Time
This lesson can be adapted to run in a single 50-minute class period, although I have most frequently introduced it in 60- to 75-minute class periods (see Table 1 for a complete teaching timeline). Homework takes from 2-5 days for students. There is a 10-15-minute follow-up segment in a future class period for instructors to give students feedback about their models.
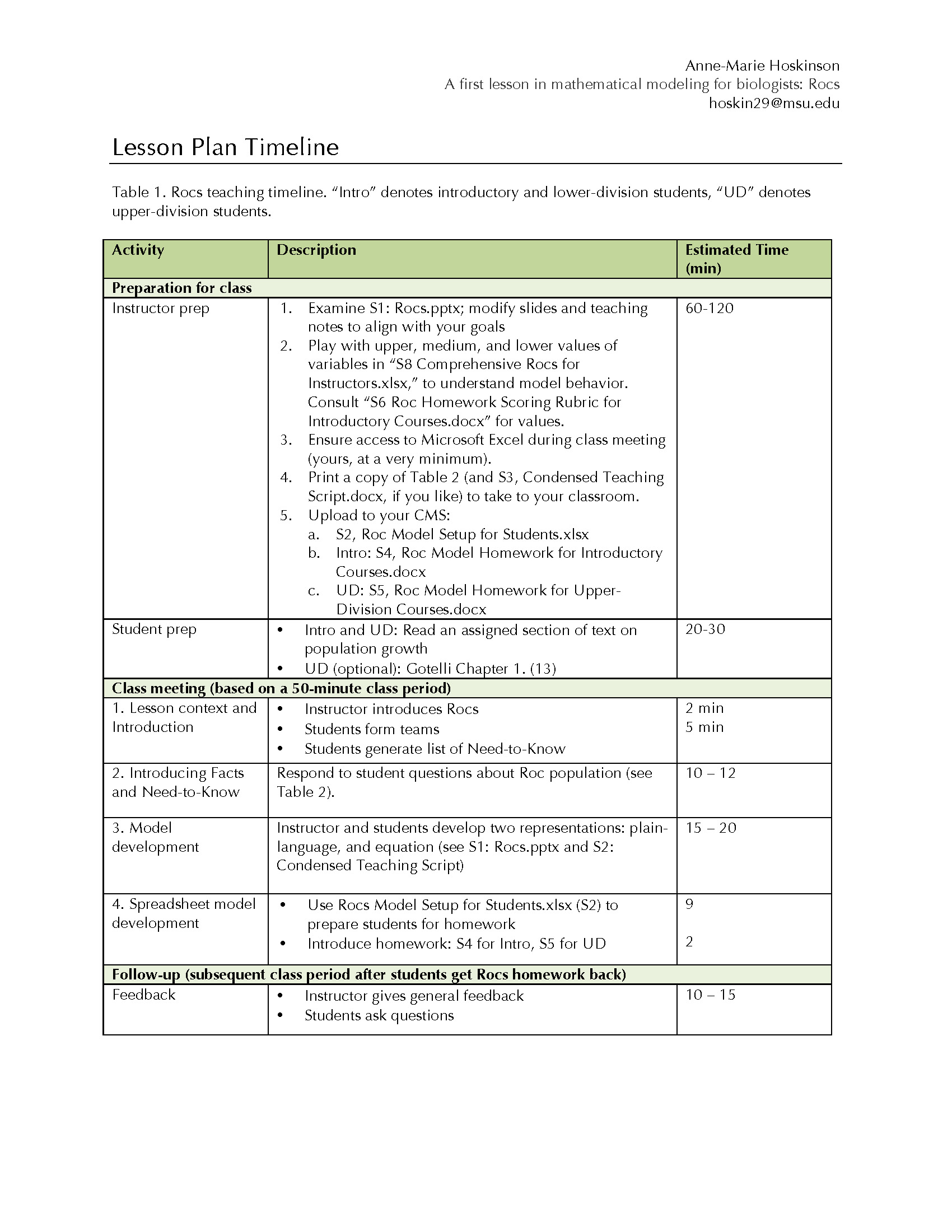
Table 1.Rocs teaching timeline. “Intro” denotes introductory and lower-division students, “UD” denotes upper-division students.
Prerequisite Student Knowledge
All students can read the chapter or section introducing population growth in whatever textbook they are using. Upper-division students might also read Chapter 1: “Exponential Population Growth” from Gotelli’s A Primer of Ecology (3rd or 4th ed.) (8). Prior experience with Microsoft Excel is helpful but not required.
Prerequisite Teacher Knowledge
Instructors should be familiar with simple exponential population models and with the use of Microsoft Excel (row and column designates, use of dollar signs for fixed cell references, creating formulas, filling down). The lesson requires no specialized mathematical knowledge.
SCIENTIFIC TEACHING THEMES
Active Learning
In this lesson, student learning occurs in small collaborative teams of three to four students. The lesson is designed so that no single student can complete the product, given the built-in uncertainty and time constraints (see Table 3). This collaboration requirement introduces students to an important feature of scientific modeling specifically, and the general processes of science: it is a collaborative enterprise. Collaborative learning, especially around problems with no "right answer," can be one of the richest forms of active learning (9). Students probe one another for understanding and explanations, make decisions about what information and facts matter most, and brainstorm about how to represent what they have created (10).
Assessment
Instructors assess student understanding of the modeling process and product by evaluating how well students' models predict the phenomenon and how well their model supports students' recommendations for managing the population.
Inclusive Teaching
Each student team's final product must be a consensus product, each student must contribute, and each student acknowledges both these ground rules when student teams turn in their reports. Invariably, student teams discover each other's strengths and weaknesses, and leverage these to accomplish the given task within the time constraints.
LESSON PLAN
Before Class Meeting
What instructors do:
You need computer access to Microsoft Excel during the lesson. Provide your students the Excel template file Roc Model Setup for Students.xlsx (Supporting File S2) for their model development through course management software (CMS). Let students know ahead of time that, for this module, they will form small cooperative teams of 3-4 that will work together in class and on homework.
Over several semesters of using and enhancing this scenario, I have embellished the details of the original myth. Each of these embellishments serves a particular purpose in helping students develop their model, described where necessary (e.g. Table 2, Table 3). Therefore, I recommend that you familiarize yourself with the scenario and not alter the details the first time you teach it. Post the homework (Supporting Files S4 and S5) on CMS prior to class. There are two versions for each file: a version geared for introductory students in large-enrollment courses and a version for upper-division students. Supporting File S1 provides a set of annotated PowerPoint slides you can use and adapt.
Although the lesson itself is structured, colleagues who have implemented this lesson have commented that they sometimes don't know what to say or ask at particular times during the class period. To meet the need for more information, the lesson plan coordinates with a short script (Supporting File S3) you can use during your class meeting or customize based on your own style and inclinations. Throughout this lesson plan, I have also capitalized, italicized, emboldened titles of key model features: Objective, Facts, Need-to-Know (as N2K), Assumptions, and Representations, to help you emphasize these features to students. This modeling framework is not introduced separately from the scenario, but embedded in it.
What students do:
The purpose of students' reading is to introduce the ideas of population modeling: that populations change in predictable ways, and that people use population models to make decisions about populations and their management. You should not assume any mathematical proficiency or understanding based on the reading. In fact, this lesson specifically assumes students are not proficient at its beginning.
During class meeting
1. Lesson context and introduction (Instructor and students, 7 minutes).
Depending on your teaching style and preferences, you may want to inform your students, briefly, that you are about to undertake a whimsical, but entirely plausible scenario.
We enter the Wayback Machine and travel back to Baghdad, Persia, in A.D. 1000. The peaceful caliphate is ruled by the benevolent and wise Caliph, who values scientific knowledge and supports a thriving and well-funded culture of research. The Caliph's librarian, Scheherazade, has come across an ancient text and painstakingly translated a passage that reads: "When the Rocs no longer fly over Baghdad, the Caliphs will no longer rule."(slide 2)
During this brief introduction, you should pause and make sure that students know where present-day Persia is, what a Caliph is, and who Scheherazade is. Do this briefly. Even in classes of as few as 40, especially given present-day events, it's unusual for at least one student not to know that Persia is roughly present-day Iraq, a caliph is, roughly, a Muslim governor, and Scheherazade was a heroine storyteller in One Thousand and One Nights. Although the details are not necessary for understanding the model or its setup, students are more likely to buy into a scenario whose details they understand. If students complain that "this isn't biology," you can remind them that context usually matters a lot in biology, so it's important to understand the context of a problem they'll be working on.
You can then continue:
Scheherazade of course takes this information to the Caliph, who, alarmed at the prospect of the caliphate ending, commissions the class - you - to advise him about the prospects for the caliphate for the next 1000 years.
The bold text on slide 2 is the model Objective. Advance to slide 3:
Scheherazade is able to tell the Caliph a few things about the life history of Rocs:
- They are enormous birds - the size of a large modern jumbo jet.
Observe whether students are writing information down. If they are not, encourage this practice; scientists record and gather facts!
- The only population is in Persia.
- Rocs nest high in the Persian desert mountains.
- The current population, at A.D. 1000, is approximately 742 Rocs.
- Each Roc builds a single nest and lays a single clutch of eggs in its 100-year lifespan.
Pause briefly and either ask who knows what a clutch is, or explain that a clutch is a collection of eggs that birds lay, all in a very short time.
- The Roc chicks all hatch on the 100(th) birthday of its parent, who then flies out into the desert and dies.
Do you have enough information to advise the Caliph about his prospects? - No!
Note that many students - and some instructors! - may automatically Assume that the Roc population is sexually-reproducing; it is not, and the use of the singular "parent" is meant to indicate this. Nonetheless, almost all students will assume that it takes two Rocs, a male and a female, to produce a Roc chick. Another implicit Assumption is often that the sex ratio is 1:1. A small number of advanced students may Assume, based on the careful language, that Rocs are asexual, which is indeed correct for this system (see Notes about Facts in Section 2). Although it may pain some instructors to let students grapple with their Assumptions, it is a critically-important lesson in modeling, particularly, and science generally, so I encourage you to allow them the opportunity to explore this. Both of these Assumptions are addressed in Section 2 and Table 2, below. Advance to slide 4.
Based on your very brief introduction to population modeling, in the next five minutes, you and your team should discuss among yourselves what you Need to Know in order to predict the Roc population in the future. Then, rank your questions, in order of priority. Scheherazade has given me access to her information to respond to your questions, but our time and knowledge is limited, so you will have to be efficient!
During the next five minutes, you can wander around your classroom to listen. Introductory students may need encouragement to keep generating ideas about what they Need to Know, based on what they have read about how scientists study populations. Importantly, do not answer questions such as "Is this a good question?" or "Do we need to know ___?" You can re-direct students to consider the question as a team. This step helps students practice gathering and prioritizing information, and communicating with one another. Since they have little experience and practice at this, some may find it bewildering or even frustrating, but it is valuable to their process of building a scientific model. Do not worry too much at this point if a few students aren't saying much with their teams.
2. Introducing Facts and Need-to-Knows (Instructor and Students, 10-12 minutes).
At the top of slide 5, write or type Objective at the top.
Every scientific model has an objective, or purpose, that defines everything people do with that model. What is the model Objective or purpose here?
Remind students of their roles as advisors, then write or type the model objective at the top of slide 5 and prompt students to write it down.
Scheherazade has given me access to Facts about Rocs. Every scientific model uses Facts, and in science, Facts are data and information. We will have ten minutes to review your questions about Facts. Use this time to gather Facts that will help you build a model that advises the Caliph. We will do this round-robin style, and I will start with this group [point]. The responses I give will apply to everyone's model, so you should all make sure to record these Facts. Listen carefully! If another team asks your question, record the answer, move down your list, and ask your next question!
Table 2 includes both Facts that are critical for building the model, and a number of non-important or irrelevant pieces of information that students nonetheless are fond of asking during the times I've taught the lesson.
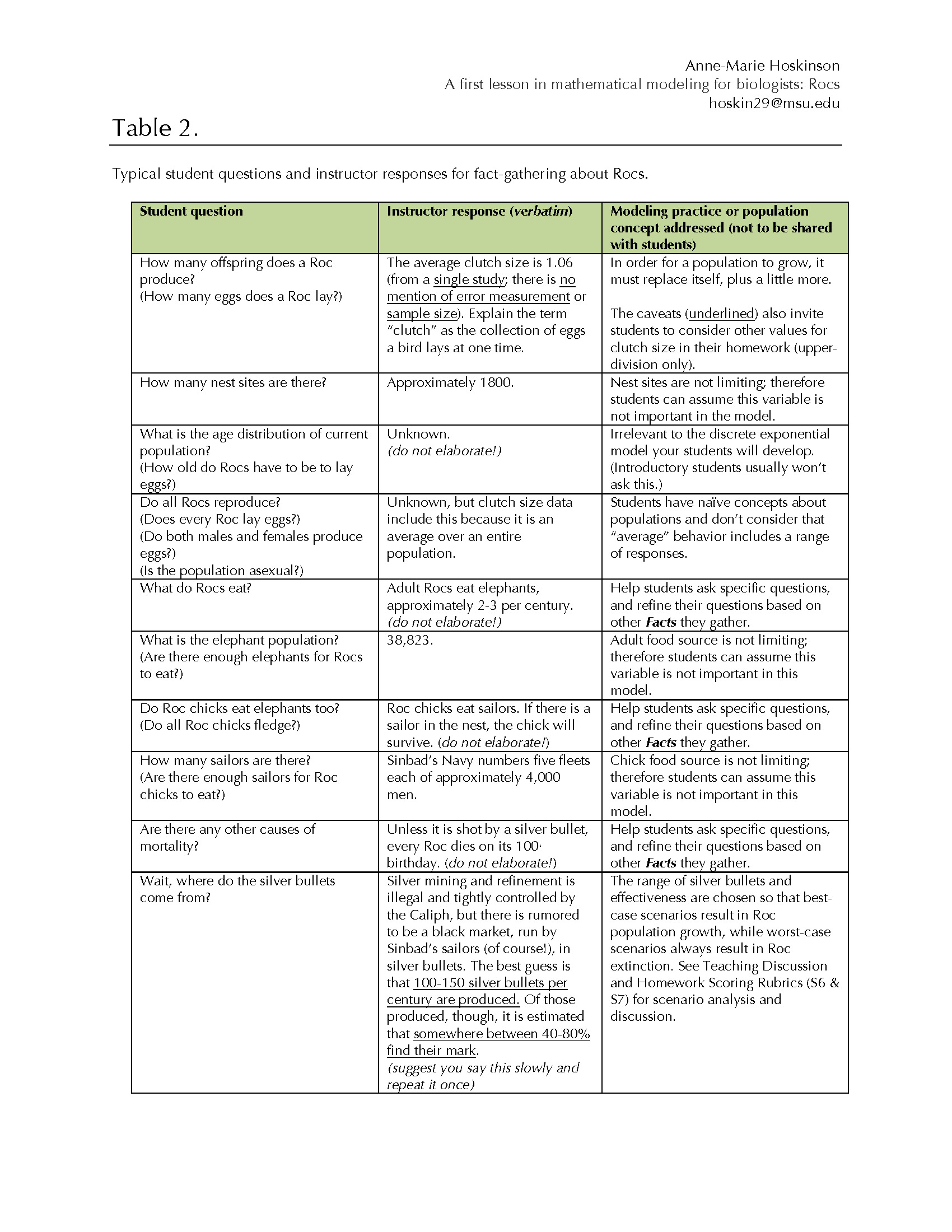
Table 2. Typical student questions and instructor responses for fact-gathering about Rocs.
To keep the process moving, call on one team at a time to ask their highest-priority question. Repeat the question for the class, to make sure everyone heard it, then provide the Fact. Keep the process moving efficiently, at a pace that keeps students on their toes but does not overwhelm them; you are the best judge of this in your classroom. Do not wait for every student to write every response down. Direct students to rely on their teams to gather and organize information as you rapidly write or type each (new) Fact on slide 5. Some student groups will ask questions that repeat information they've already been given, or ask irrelevant or even absurd questions. Treat every question seriously, and provide a plausible response that does not affect the model (see Notes about Facts and Section 3, Model Development, below).
After eight minutes, if critical questions about chick food source and other causes of mortality (Table 2) have not yet been asked, you can ask, "Don't you Need to Know about _____?" If three student groups ask seriously off-topic questions in a row, you can pause and ask the class to think for a few moments about what factors are important to any population growing or declining, to get them thinking about food and causes of mortality.
Notes about Facts. The Facts are chosen so that this population meets the Assumptions for a discrete, exponentially growing population. Those Assumptions are as follows: (8)
- This population is asexual (all individuals can produce viable offspring). The variable "clutch size" is a population-level metric: it applies equally to all individuals. Some Rocs will have no chicks, some will have two, and some will have many more, but the mean for the population starts at 1.06 chicks per Roc. Similarly, metrics such as "age of first heart attack" applies to all individuals in a population: some will have heart attacks earlier, later, or not at all, but the mean of all of these observations applies to the entire population.
- Neither nest sites nor adult or chick food sources are limiting. (This is sometimes dubbed the "paradise" Assumption.)
- There is no age or genetic structure. Practically, this means that all individuals can reproduce the moment they are born until the moment they die, and that all are equally fecund.
- The population has a discrete generation time of 100 years.
What elevates this model from a trivial model with a single solution to a simple but non-trivial model is the constrained uncertainty in silver bullets coupled with clutch size (Table 2). These are the only two variables in the model you will help students develop (Section 3, Model Development). In the lesson as presented, I've chosen variable values so that the ranges include the equilibrium (see Teaching Discussion), but depending on the upper and lower bounds (S4 and S5, Homeworks) some scenarios will show the Roc population increasing or stable, while other scenarios will result in the Roc population declining, in some cases to extinction. I recommend that instructors plug the upper, medium, and lower values for the variables into S8, Comprehensive Roc Model Setup for Instructors.xlsx, to explore how the model behaves before you teach this lesson. In upper-division courses, you will not tell students which scenarios to explore.
3. Model Development (Instructor and students, 15-20 minutes).
Students at all levels first develop a plain-language Representation using everyday, non-technical language. I explain the term "discrete" to mean that individuals in a population all reproduce at a specific time. Ask students to think of real organisms with discrete generations (examples include salmon, annual grasses and flowers, mayflies and many other aquatic insects, white-tailed deer, elk, and wolves). You can contrast that with continuous population models and ask what organisms might better be described by a continuous model (examples: humans and some other primates). Rocs have discrete generations; ask students to review their Facts for what the generation time is (100 yr; slide 6). They should see that the models they will build must get them from this generation to the next one in 100 years, then the one after that, and so on, over ten generations, to 1000 years in the future.
Ask students, in their teams, to write out a statement in plain language that describes how "Rocs in the next generation" result from "Rocs in this generation" (slide 7). Some students will want to go immediately to writing an equation. There are two reasons to discourage this practice. First, I have never had a student do this correctly the first time. Second, equations are not meaningful to all or even most students yet. By building a verbal Representation first, students can be metacognitive about their Representations. You can even prompt them to consider why you didn't start by writing an equation.
Ask 2-3 student teams to share their plain-language Representation, and write or type these on slide 8.
Next, you will prompt students for ways to represent mathematical variables. With introductory students you might simply say,
Let's use the letter little-t for the generation time of 100 years. Then, t represents now, or the starting time; t+1 is one generation from now, or 100 years from now. Let's use capital-R to stand for the Roc population. So how will we Represent "Rocs in the next generation?"
Rt+1. [You should write or type this on slide 10.]
Similarly, how will we write "Rocs in this generation"?
Wait for some students to respond.
Rt. [You should write this to the right of Rt+1 on slide 10; leave space between the two.]
How do we represent "will be" in math language? - equals sign. [Write or type that between Rt+1 and Rt.
How will we think about the next part, "...that didn't get shot by silver bullets..."?
Wait for students to respond: subtract or take out the Rocs that get shot. Encourage them to use whatever language they're most comfortable with, even colloquial language, because it helps them develop conceptual understanding of the population first.
But notice that we have silver bullets, when what we really need are Rocs that don't get shot. How will we figure that out?
Wait for students to respond. Depending on your reading of your introductory course population, you may simply need to explain that we will call that variable "effective silver bullets." Those are the silver bullets that are produced, then find their marks, killing a Roc (see Table 2). With that, we now have the same units (Rocs) for both R and s. Now you can write or type on slide 10:
Rt+1= Rt - s
If we add nothing else to this population, what's going to happen?
Students should be able to see that it declines to zero eventually.
Our model needs one more variable: what is it? - Yes, Rocs reproducing. Do we have that Fact? What is that Fact? - Yes, clutch size. Let's denote that with a little-c.
Rt+1= (Rt - s)*c Eq. 1 (slide 11)
Tell students to write this in their notebooks. This is the Representation of their model, and they will need it for their homework (slide 12).
If students say or ask, "Wait, what about chicks getting shot?" or "Does every chick that doesn't get shot lay a clutch of eggs?" draw their attention to the Facts they just gathered from Table 2. For instructors, remember that a population's clutch size is an average for all individuals in that population. For our purposes, then, it does not matter whether the population is sexual or asexual, although the simple discrete exponential model we are using, Assumes a population is asexual. For other questions, refer to the careful language in Table 2 and re-iterate those responses. You should be fully prepared to have uncertainty and some confusion from students; this is by design.
4. Spreadsheet model development (Instructor or Instructor and Students, 11 minutes).
Students in both introductory and upper-division courses will use Roc Model Setup for Students.xlsx (S2). Introductory students' homework (S4) is structured such that model-building (scenarios in Excel) and model-using (prediction and decision-making) are constrained to limit the chances that students will make unproductive or bewildering mistakes. Introductory students will choose among given and suggested scenarios to explore in their homework, and their model product will differ. In smaller upper-division courses with more advanced students, the scenarios are not pre-determined, but the decision-making process is still constrained in their homework (S6-please email hoskin29@msu.edu for rubric). Even at this level, students lack experience using data and models to make decisions.
Open the Excel workbook, Roc Model Setup for Students.xlsx (S2). If you allow laptop computers in your course, you can have students open it at the same time. If you do not normally allow laptop computers, I recommend you make an exception for this class period only, so that students can follow along, make mistakes, and practice correcting their mistakes before they tackle the homework.
On the single worksheet, there are three areas to orient your students:
- Model variable values, top left (cells B1 & B2, E1 & E2).
- The model itself, which will run in cells C7-C17.
- A pre-made, uncaptioned figure.
Although the student version comes without values inserted, there is also a Comprehensive Rocs for Instructors (Supporting File S8). This version comes with two worksheets: the model worksheet, titled Rocs, and a worksheet title Figure.
Model Variable Values
Ask students what the clutch size Fact is. You can type in "1.06" in cell B1. Remind students that this number is from a single study; there is no mention of error measurement or sample size. Typically at this level, they do not know the resulting implications, so you should suggest that they try values "slightly more or slightly less than" the given value, or about 1.02 to 1.10. (Many students at this level think "slightly more" is 2.0.) In all cases, once students have a final value for their model, they can simply delete variable values from the given cells and enter new values to try. If they make a serious mistake, they can always exit the Excel workbook without saving changes, then re-open it.
Ask students what the starting population is and show them where to enter that (E1).
The Model
Although this is a straightforward matter of translating Equation 1 into Excel, it is not simple for many students. Show students the Formula Bar. Type 742 in cell E1 for starting population.
All formulas in Excel begin with an equals sign.
I will put my cursor in cell C7, I'll type "equals E1." Notice how our initial population appears in C7. Let's go up here to E1 and change that, and notice how it changes in C7 as well. That will be helpful for you exploring how your model responds to different values for each variable.
Our model will run down here in the cells C7 through C17. In cell C7, notice I just have the starting population.
Now let's move down to cell C8, where we want to calculate the population in the year AD 1100. From our Representation in Equation 1, which cell contains the number of "Rocs in the last generation"? Yes, C7.
Put your cursor in cell C8 and type =C7, then the minus sign.
Now, which cell contains the number of Rocs "shot by silver bullets"? - Yes, B2.
Type "-B2."
Which cell contains the number of Rocs that reproduce? - Yes, B1, the clutch size. But, we want to multiply "Rocs that survive" by the number of Rocs that reproduce, so let's put parentheses around C7-B2.
Your formula bar should now contain "=(C7-B2)*B1".
Now, we could type that eight more times, or we could use an automatic copy/paste function. So do that.
Show students how you float your cursor over the bottom-right corner of the cell until the cursor turns into a thick black crosshatch, then click and hold the mouse button, then drag down.
What, that didn't work? We need to make a couple of small changes. In cell C8, type a dollar sign in front of BOTH the letter B and numeral 1, then in front of the letter B and numeral 2. This is called an absolute reference in Excel, and it means that every time our model runs, the equation will always refer to those two exact cells.
Then you can copy and paste, or drag down to C17. Put your cursor in a lower cell to show students that the model will always refer to the same cells for clutch size and silver bullets (since these values don't change with time), and to the final population from the previous generation.
And notice that the worksheet filled in "Final Pop" up here in E2, so you can easily compare the starting and ending populations.
The Figure
Notice that there is now a trendline in the figure. You'll find this line helpful when you summarize the overall patterns. On your homework, your team will give this figure a specific, descriptive caption.
Do not explore other scenarios with students at this time. Introductory students have 9 scenarios to explore on their homework; upper-division students will be prompted to think about upper and lower bounds.
Homework Setup
Conclude with your normal routine of showing students where you've placed the homework on your CMS and when it is due (see last row of Table 3 for suggestions). Point out to students that they have a lot to accomplish in little time. Often, scientific models are the best we can do given limited resources, including time.
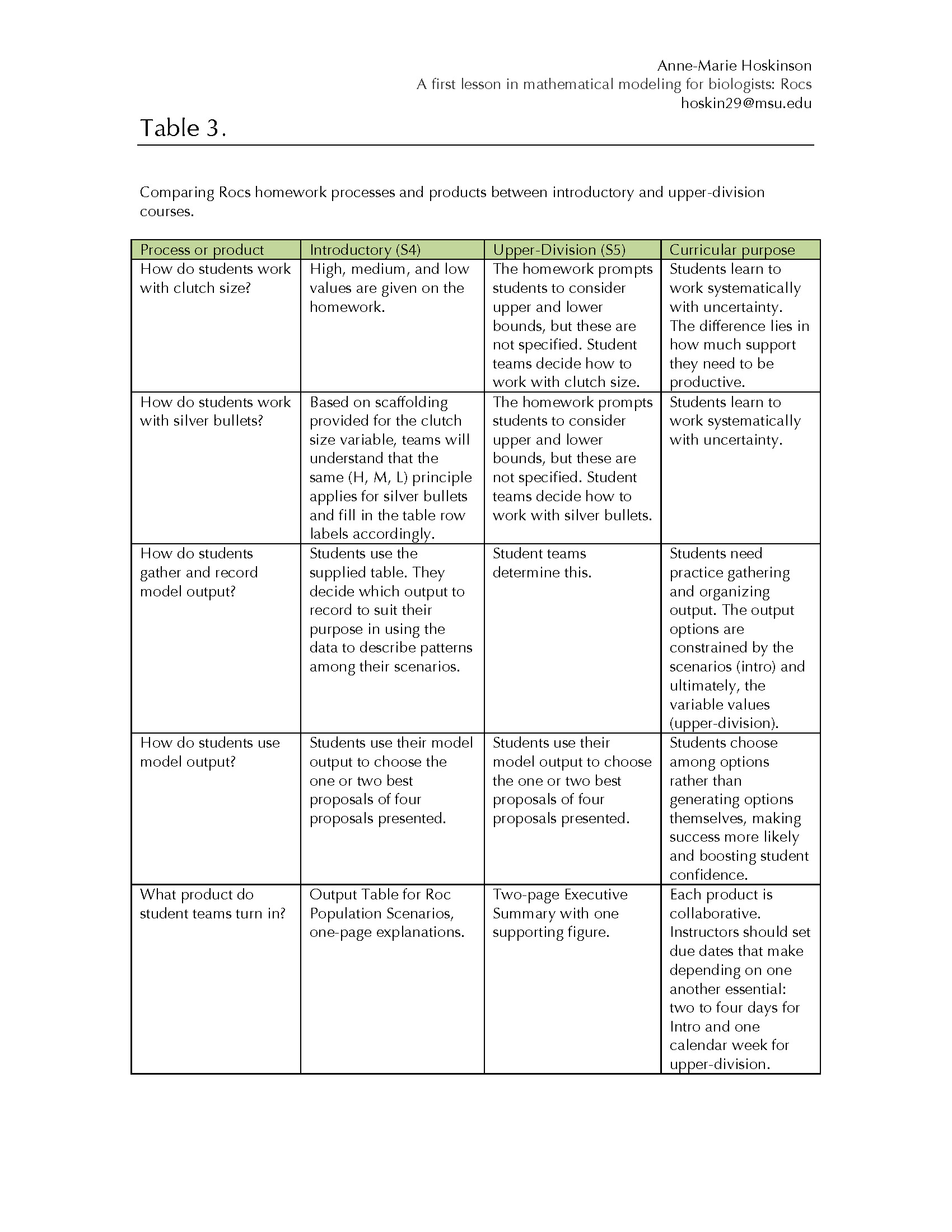
Table 3. Comparing Rocs homework processes and products between introductory and upper-division courses.
After class meeting - Follow-up
Set your class due date based on the recommendations in Table 3 (last row). The due dates are ambitious, with the intention of limiting a modeling resource - time - that is typically one of the limiting resources for real-world scientific modeling. Mention this to students. Typically students find that meeting the suggested due date is challenging but realistic.
Use the scoring rubric for the specific homework (Introductory: S6 and Upper-division: S7-please email hoskin29@msu.edu for rubrics) to evaluate or score your students' work. These scoring rubrics are meant to be used by both instructors and students. Each scoring rubric has two purposes: 1) to illustrate to instructors how to score and give feedback on these products rapidly and systematically; and 2) to provide students feedback on the most common errors, which the model and assignment have been designed to elicit (see S6 and S7, blue text, for thorough consideration of common mistakes-please email hoskin29@msu.edu for rubric). In large classes, it may be unrealistic to score all of the submitted assignments. By evaluating a subset of responses, you can still collect useful information from the homework about what your students are thinking. If it is possible, return your students' work to them. In a subsequent class meeting, you can offer feedback about the most common mistakes. Depending on your course objectives, you may find it instructive to lead your students through an in-class peer evaluation using the scoring rubrics in a subsequent class meeting.
TEACHING DISCUSSION
This lesson plan is its own model of a modeling lesson plan. The main objective of this lesson plan is to give students experience in actually building a non-trivial scientific model, within constraints that increase their chances of success. For novices, those constraints include using a relatively easy-to-use tool (Microsoft Excel) and choosing among a small set of options for their model input and output. The short follow-up includes instructor feedback to students about some potentially critical and common mistakes students often make.
There are (at least) two pedagogical challenges. First, you must keep the lesson moving and keep students on task and helping one another, even when they are uncertain - and uncertainty is a deliberate and prominent part of this model. Be clear in your own mind of the value of students grappling productively with uncertainty; this is why it is a Learning Goal. Uncertainty - and discomfort with it - may be especially apparent in your introductory courses. Students in upper-division courses seem to have a greater capacity for tolerating it. Reassure students that this helps them become better thinkers and that you are not trying to trick them. Few students have ever had to confront ranges of variable values; decide how to solve a problem; solved a problem with multiple solutions and interpretations; or use their output to make a real decision. The inherent uncertainty also makes collaboration not just a convenience or a good idea, but essential to students' success. To reassure students and reinforce the importance of making productive mistakes, I often score introductory students' homework for completion only.
Second, this lesson is built to funnel students into making a set of systematic mistakes that typically get in the way of understanding population models. You can see from the scoring rubrics (S6, S7-please email hoskin29@msu.edu for rubrics) that students often make assumptions without testing them, and sometimes make assumptions without knowing they are doing so. This (Assumptions) is a difficult principle for even advanced modelers to master fully; some breakthroughs in science occur when people reconsider a model's Assumptions. (7) The lesson is also designed so that students develop deep understanding about how populations behave and how different factors can interact in unexpected ways. By investing more time in developing the model at the beginning of a module about populations or modeling, students gain experience and confidence building and evaluating models. They begin to learn that scientific models are not right or correct, but useful and improvable.
This lesson as written presents carefully chosen values for each of the variables of effective silver bullets and clutch size. The following discussion is for instructors, not students, although instructors whose objectives include model equilibria with upper-division students can certainly use the following discussion in their planning for a follow-up lesson. Our model's behavior is governed by just three variables: starting population R0 (only upper-division homework asks students to consider this as a variable), clutch size c, and effective silver bullets s. Given a starting population and either a constant clutch size c or constant effective silver bullets s, you can calculate any scenario's equilibrium, where Rt+1 = Rt = R0.
If clutch size is held constant, then equilibrial effective silver bullets will be given by:
s = - ((1-c)/c)R0 (Eq. 2)
If silver bullets are held constant, then equilibrial clutch size will be given by:
c = (R0/(R0-s)) (Eq. 3)
If you teach this lesson repeatedly, you may want to change variable values to discourage students from searching for old versions of the model and its output. Using Equations 2 and 3, you can choose plausible ranges of variable values that include an equilibrium. The implication for students is that their model output will show the Roc population increasing under some scenarios, and decreasing, sometimes to extinction, under other scenarios.
SUPPORTING MATERIALS
- S1. Rocs lesson presentation slides (Rocs.pptx)
- S2. Rocs student Excel worksheet (Roc Model Setup for Students.xlsx)
- S3. Roc lesson teaching script (Roc Condensed Teaching Script.docx)
- S4. Roc Homework for Introductory Courses.docx
- S5. Roc Homework for Upper-Division Courses.docx
- S6. Roc Homework Scoring Rubric for Introductory Homework.docx-please email hoskin29@msu.edu for rubric
- S7. Roc Homework Scoring Rubric for Upper-Division Homework.docx-please email hoskin29@msu.edu for rubric
- S8. Roc instructor Excel workbook (Comprehensive Rocs for Instructors.xlsx)
ACKNOWLEDGMENTS
I am ever grateful to Dr. Tony Starfield, who taught me the principles and the art of building scientific models, and from whom I learned my most important question: What's the purpose? I also thank Robin Wright and two anonymous reviewers, whose comments and suggestions substantially improved the manuscript and its supporting files. Finally, I thank the hundreds of students whose first model in my courses was Rocs, for their patience, humor, and willingness to make mistakes. Their questions and feedback had the greatest effect in developing this lesson.
References
- Passmore, C. M., and Svoboda, J. (2012). Exploring opportunities for argumentation in modelling classrooms. IJSE 34, 1535-1554.
- Hoskinson, A.-M. (2010). How to build a course in mathematical-biological modeling: Content and processes for knowledge and skill. CBE-LSE 9, 333-341.
- Brewer, C. A., and Smith, D. (2011). Vision and Change in Undergraduate Biology Education: a Call to Action (Washington DC: American Association for the Advancement of Science).
- Bereiter, C., and Scardamalia, M. (2010). Can children really create knowledge? Can. Journ. Learn. & Tech. 36, 1-15.
- Vosniadou, S. (1994). Capturing and modeling the process of conceptual change. Learning and Instruction 4, 45-69.
- Dunbar, K. (2000). How scientists think in the real world: Implications for science education. Journal of Applied Developmental Psychology 21, 49-58.
- Hoskinson, A.-M., Couch, B. A., Zwickl, B. M., Hinko, K. A., and Caballero, M. D. (2014). Bridging physics and biology teaching through modeling. Am. J. Phys. 82, 434-441.
- Gotelli, N. J. (2008). A Primer of Ecology 4 ed. (Sunderland, MA: Sinauer).
- Hakkarainen, K., Pavlova, S., Kangas, K., and Seitamaa-Hakkarainen, P. (2013). Sociocultural perspectives on collaborative learning: Toward collaborative knowledge creation. In The International Handbook of Collaborative Learning, C. E. Hmelo-Silver, C. A. Chinn, C. Chan, and A. M. O'Donnell, eds. (New York: Routledge), pp. 57-73.
- Shell, D. F., Husman, J., Turner, J. E., and Cliffel, D. M. (2005). The impact of computer-supported collaborative learning communities on high school students' knowledge building, strategic learning, and perceptions of the classroom. Journal of Educational Computing Research 33, 327-349.
Article Files
Login to access supporting documents
A first lesson in mathematical modeling for biologists: Rocs(PDF | 201 KB)
S1. Rocs-Lesson presentation slides.pptx(PPTX | 548 KB)
S2. Rocs-Student Excel worksheet-Model setup for students.xlsx(XLSX | 12 KB)
S3.Rocs-Condenced teaching script.docx(DOCX | 135 KB)
S4. Rocs-Homework for intro course.docx(DOCX | 103 KB)
S5. Rocs-Homework for upper division course.docx(DOCX | 94 KB)
S8. Rocs-Instructor Excel workbook-Comprehensive Rocs for instructors.xlsx(XLSX | 18 KB)
Table 1.jpg(JPG | 499 KB)
Table 2.jpg(JPG | 684 KB)
Table 3.jpg(JPG | 520 KB)
- License terms

Comments
Comments
There are no comments on this resource.