A Hands-on Introduction to Hidden Markov Models
Published online:
Abstract
In this Lesson, we describe a classroom activity that demonstrates how a Hidden Markov Model (HMM) is applied to predict a eukaryotic gene, focusing on predicting one exon-intron boundary. This HMM lesson is part of the BIOL/CS 370 'Introduction to Bioinformatics' course (Truman State University, MO) and of Bio4342 'Research Explorations in Genomics' (Washington University in St. Louis, MO). The original target student audiences include both Biology and Computer Sciences majors in their junior and senior years, although we believe the model activity would be successful with younger students. The class session starts with a brief introductory lecture describing HMMs and the terminology used in defining the parameters for a given model. This lecture is followed by students' exploration of the HMM using Excel spreadsheets to manage calculations while they alter the key variables; collaborative problem solving and discussion of their strategies and results; and homework to check their understandings.
Students have reacted very positively to the HMM curriculum. Students with more computer science experience tended to ask more questions concerning the model itself. Overall, students performed well on the homework assignment, leading us to believe that we are a step closer to our main goal of filling the intellectual gap between computer scientists and biologists.
Citation
Weisstein, A.E., Gracheva, E., Goodwin, Z., Qi, Z., Leung, W., Shaffer, C.D. and Elgin, S.C.R. 2016. A Hands-on Introduction to Hidden Markov Models. CourseSource. https://doi.org/10.24918/cs.2016.8Society Learning Goals
Bioinformatics
- DNA - Information Storage [GENOMICS]
- Where are data about the genome found (e.g., nucleotide sequence, epigenomics) and how are they stored and accessed?
- How can bioinformatics tools be employed to analyze genetic information?
Genetics
- Methods & Tools in Genetics
- What experimental methods are commonly used to analyze gene structure and gene expression?
Science Process Skills
- Process of Science
- Pose testable questions and hypotheses to address gaps in knowledge
- Construct explanations and make evidence-based arguments about the natural world
- Modeling/ Developing and Using Models
- Build and evaluate models of biological systems
- Communication and Collaboration
- Share ideas, data, and findings with others clearly and accurately
Lesson Learning Goals
- Students will understand the basic structure of an HMM, the types of data used in ab initio gene prediction, and its consequent limitations.
- Students will understand the process of gene exon-intron boundary prediction, having altered the values for the key parameters and noted the impact on the prediction.
- Students will consider how the exon-intron boundary model might be designed to be more accurate, thinking about the biological features of the process and how they might be represented in a computer program.
Lesson Learning Objectives
- Students will be able to process unannotated genomic data using ab initio gene finders as well as other inputs.
- Students will be able to defend the proposed gene annotation.
- Students will reflect on the other uses for HMMs.
Article Context
Course
Article Type
Course Level
Bloom's Cognitive Level
Vision and Change Core Competencies
Vision and Change Core Concepts
Class Type
Class Size
Audience
Lesson Length
Pedagogical Approaches
Principles of How People Learn
Assessment Type
INTRODUCTION
In recent years, the biological community has entered the Age of Genomics. With vast amounts of sequencing data, as well as many other types of "big data" becoming available, we clearly need to expand and modify the existing educational programs to prepare biologists and computer scientists to talk with each other; we need to prepare interested computer scientists to think like a biologist and vice versa. The problem is that even today, many Biology majors view mathematics and computer science as difficult subjects to avoid if possible, while many Computer Science (CS) majors lack exposure to advanced biology. Numerous colleges and universities, including those of the co-authors, have worked to close this gap by developing programs in bioinformatics, including those of the co-authors. To develop student appreciation for the use of computers in biology, Washington University in St. Louis organized the Genomics Education Partnership in 2006, engaging students in a large-scale genomics project centered on the annotation of novel genomes (1,2). Today GEP unites over 100 colleges and universities nationwide, with students from over 60 schools actively participating in a GEP annotation project during 2014 - 2015. To be intelligent users of bioinformatics tools, students must learn about the underlying algorithms.
Here we present a Lesson 'A Hands-on Introduction to Hidden Markov Models' developed primarily by Dr. Anton Weisstein (Truman State University, MO) and Zane Goodwin (TA in Bio 4342, Washington University in St. Louis), with contributions from the other co-authors. This Lesson is based on the original publication, 'What is a hidden Markov model?' by Sean Eddy (3, S1). The lecture and exercise introduce students to the idea of the Hidden Markov Model (HMM), which forms the core component of many gene predictors. Hidden Markov Models are a set of mathematical tools that can be used to draw inferences about genomic and evolutionary processes, where we cannot see the original state but can see the current product. In general, an HMM calculates the probability of each scenario that could have resulted in an observed data set, and then uses statistical methods to identify the most likely scenario. For example, HMMs can be applied to DNA sequence data from different species to infer the likely pattern of relationships among those species (4). The example in this Lesson comes from ab initio gene finding, focusing on just one decision: predicting the point of transition from an exon to an intron, i.e. a splice site donor.
This HMM introduction is part of our mid-level bioinformatics courses. Students taking "Research Explorations in Genomics" or "Introduction to Bioinformatics" courses are usually Biology or Computer Science (CS) majors. Of the 26 students enrolled during the fall semester 2013 at Truman State, 14 were Biology majors and 12 were CS majors. The Hidden Markov Model was introduced during week 12 of a 15-week course, as part of the section on gene finding. By this point, the students have already studied gene and genome structure, models of molecular evolution, and common techniques for sequence alignment and phylogenetic reconstruction (including likelihood-based methods that served as an introduction to probability calculations). At Washington University in spring 2014, 11 of 15 students were Biology majors, with the remainder majoring in Biochemistry. The HMM unit was introduced after students had significant experience annotating genes, working with the results of ab initio gene finders as well as conservation patterns and RNAseq data.
HMM class materials include the set of introductory lecture slides and the Excel workbook "Hidden Markov Model" (see Supporting Files S2-S10) that illustrate the mathematical workings of an HMM. The Excel workbook uses Eddy's (3) example of recognizing the most likely 5' splice site within a DNA sequence based on the probabilities of the different state paths (3). By manipulating model parameters such as the average length of exons and introns (i.e. adjusting the HMM model transition probabilities) and the difference in base composition between exons and introns (i.e. adjusting the HMM emission probabilities), as well as changing the underlying DNA sequence, students can investigate how these changes influence the model's decisions about where the splice site is most likely to occur. The Excel worksheets will do the needed calculations for the user, thereby enabling students to explore a range of values for each parameter fairly quickly and to focus on the impact of these changes instead of the arithmetic.
The students spent approximately one 60-minute class period on HMMs, which included an introductory lecture, time to explore the model, several problems for students to solve in small groups, and discussions of their strategies and results. At the end of class, students received a brief homework assignment to test their understanding of the basic HMM concepts and their applications in large-scale genome sequencing projects. This assignment required students to have access to Excel outside of the class period.
SCIENTIFIC TEACHING THEMES
Active Learning
During the class, students engaged in manipulating the model and discussing the outcomes. Active learning strategies included collaborative problem-solving and subsequent discussion, as well as open-ended questions about potential complications in using HMMs.
Inclusive Teaching
To help both CS and Biology students achieve a complete understanding, the class instructor presented HMMs in multiple ways: graphically, mathematically, and verbally. At Truman, students with different backgrounds were assigned to the same discussion group; in particular, the Biology majors were paired with students co-majoring in math.
Assessment
Formative assessment included monitoring each group's progress during class and steering student discussions as needed, then facilitating a class-wide discussion. At Truman, summative assessment was a question on the take-home final that students were required to work individually. The question asked students to apply HMM methods to a novel system (i.e. inferring the location of an alpha helix within a given amino acid sequence). Approximately 60% of students were able to estimate relevant parameter values and correctly calculate both the probability and the likelihood of a specific state path, while 70% were able to articulate the difference between these two measures. At Washington University, the students' understanding of the HMM was assessed by reviewing the results of the homework (S7). The results are shown in Figure 1. Overall, students were able to solve the problem correctly in 90% of the cases. Question 1a, which only 53% of the students answered correctly, required the students to draw a state diagram for an HMM that scans an un-annotated genome for genes with a start codon, a stop codon, exons, introns, a 5' splice site and a 3' splice site. Collectively, the results from both universities suggest that the students had more difficulties in extrapolating the model (i.e. extending it to a new situation) than they had in using the model.
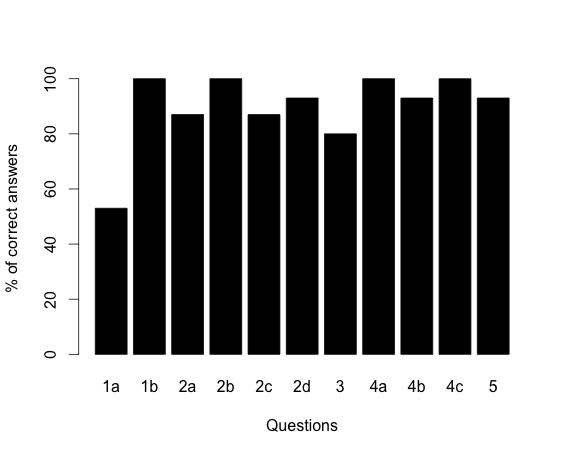
Figure 1. Tally of the HMM homework results. Numbers along the X-axis correspond to the homework questions (Supporting material). Bar graphs indicate the percentage of satisfactory or above satisfactory answers.
We believe that any assessment should include a component that measures students' ability to apply the methods they have learned to a substantially different system. However, this expectation would be more meaningful as part of a larger, integrated research-like project than as a stand-alone exam problem. We also think that assessment should explore students' understanding of why and how HMMs work, focusing on specific aspects that were not directly addressed in the exercise (e.g., how to optimize the transition and emission probabilities of each state).
LESSON PLAN
The class session takes place in a room with one large table, or tables suitable for sub-groups. Lecture slides are projected on the board. Students have access to computers (laptops).
Students in Bio 4342 are required to read 'What is a hidden Markov model?' by Sean Eddy (3) prior to class. The paper is relatively short and is well-designed for non-CS readers.
The lesson plan is presented as a flowchart (Figure 2). Class starts with a brief introductory lecture followed by discussions and collaborative work.
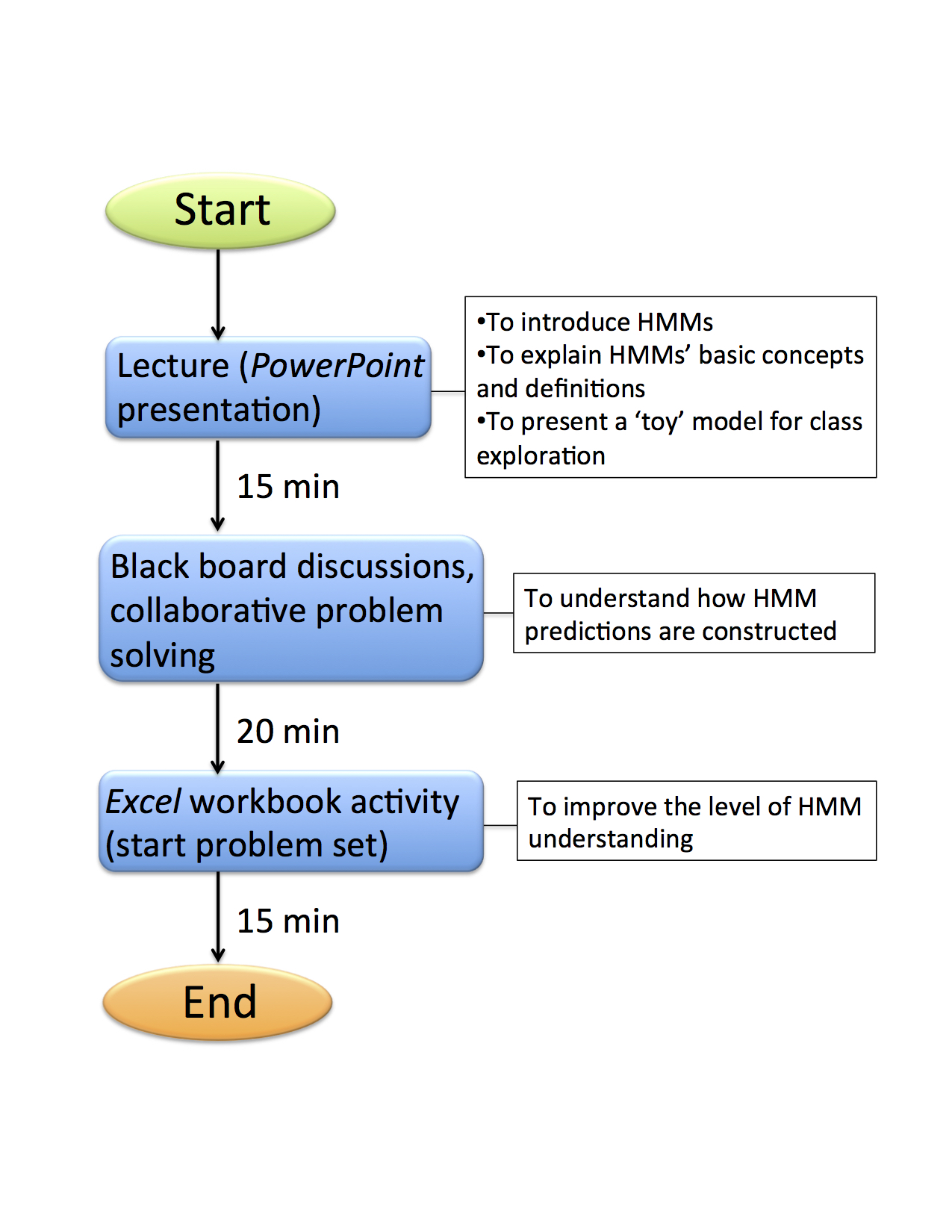
Figure 2. Timeline for Introduction to Hidden Markov Models Class Activities.
The lecture on HMM fundamentals is aimed at giving students a basic intuition for how ab initio gene finders identify genes within a genomic sequence. The lecturer introduces the types of problems that an HMM is designed to solve, as well as the different components of an HMM, including transition probabilities, emission probabilities, and state machines.
There are various ways to make students confortable with the probabilistic nature of the HMM. We include two PowerPoint presentations that were used as the HMM introductory lecture at Washington University. Both presentations were designed for students with similar background knowledge. One of the presentations (by Zane Goodwin) focuses primarily on the material from the Eddy paper (S1, S3). Because the students were assigned to read the Eddy paper before class, the instructor can assume that the students are already familiar with the HMM 'toy' model diagram. This pre-reading enables the instructor to spend more time on explaining how different elements of the system work. This approach also teaches students to be more confident when reading conceptual scientific publications. The second presentation (by Zongtai Qi) provides broader background information on HMMs, using weather prediction (a common choice) to introduce the concepts of hidden states and state transition probabilities before turning to the splice site prediction model. This presentation also provides a detailed explanation of the components in the 'toy' HMM model and the probability calculations for each state path (S4).
A critical aspect of the introduction is developing an understanding of how the state path probabilities are calculated. Dr. Weisstein uses a six nucleotide-long DNA sequence as an example to illustrate the states, transition and emission probabilities, and the probability associated with each state path in order to identify the most probable state path. All calculations are done manually on the board with active student participation (lecture video recording is available at Genomics Education Partnership website http://gep.wustl.edu/media/weisstein-hmm-lecture). The close interactions between the instructor and students help ensure the success of each student when they are 'playing' with the simple HMM example subsequently using the Excel workbook (S6, S10).
Students are then introduced to the Excel workbook. For ease of demonstration, the workbook begins by analyzing a very short sequence before re-creating Eddy's full, 26-bp model. The first sheet in the workbook, appropriately named "Simple Model," demonstrates the calculations involved in using the parameters of the HMM to determine the most likely splice site location (Figure 3). The user enters a short DNA sequence and sets the model parameters in the Excel worksheet, which uses these values to compute the likelihood of each potential 5' splice site location. The workbook and step-by-step instructions are provided in the S5. Based on the reflections from the Bio 4342 students at Washington University in St. Louis, we suggest that the instructor starts this activity with the Excel spreadsheet projected on the board and walk through the first worksheet, perhaps stopping at cells that are most crucial to creating the predictions. It would also be beneficial to make students aware that the homework contains questions that are based on the Excel workbook activity.

Figure 3. The Excel workbook “Hidden Markov Model” illustrates the mathematical workings of an HMM, using Eddy’s (2004) example of locating the 5’ splice site within a DNA sequence.
After completing the exercises associated with the "Simple Model" as a group, students move to the "Full Model" sheet, which uses the exact sequence and parameters as the Eddy publication (3); at this point students are expected to be working mostly individually.
TEACHING DISCUSSION
A Hidden Markov Model is a type of a probabilistic finite state machine (FSM) that consists of a set of states with different emission and transition probabilities. HMM is a supervised machine learning technique that was initially used in the 1970's to address the computational problem of speech recognition. Today, it is a very commonly used tool in computational biology, forming the basis of many bioinformatics tools routinely used by life scientists (e.g., sequence alignment, gene finding, transcription start site identification, protein structure prediction). Hence the HMM is an indispensable tool for the primary annotation and analysis of growing volumes of genomic data.
In introducing the HMM, our main goals have been to help our students understand how the computer utilizes biological data and how the initial processing of a newly sequenced genome is done. A secondary goal is to teach future biologists and computer scientists to speak the same language and to work effectively together.
This HMM lesson gives students a basic introduction to how gene finders predict gene models within a genomic sequence. It also gives them some familiarity with how probability is used in gene finding. In addition, it illuminates the assumptions and the limitations of using an HMM to capture the complexity of eukaryotic genes, which helps explain the low accuracy of many gene predictors. Understanding the assumptions that an algorithm makes is a key thought process of computational thinking that not all biologists are familiar with, and we think the students learned this thought process well using this Lesson.
One challenge is trying to help the students understand that an HMM can take many different forms, depending on the application. To illustrate this, we developed the simple six-nucleotide model discussed above, with the thought that this simplistic model would demonstrate how an HMM works without making the model too complex. The addition of more features to an HMM (e.g., additional states, higher-order HMMs) will make the HMMs more accurate but also much more difficult to grasp at a conceptual level. However, some students took the simple model too literally and openly critiqued the approach based on this simple example. This experience illustrates a common challenge: to explain how a model works in a simple manner without sacrificing accuracy. The trade-offs between the complexity and the accuracy of the model are relevant to most bioinformatics analysis. Exposure and discussion are important in training computer scientists (seeking practical solutions) and biologists (seeking accuracy) to interact with each other in order to find the best solution that is also computationally feasible.
With regard to the problem of parameter optimizations, this HMM lesson provides the students with a general grasp of how biological observations can be transformed into parameters for an HMM-based gene model in theory. However, many of the practical details of this process [e.g., cross-validation, receiver operating characteristics (ROC) analysis] were omitted for the sake of simplicity. Even without the practical details, we think the HMM lesson helps to bridge at least part of the gap between biologists and computer scientists.
SUPPORTING MATERIALS
- S1: Hidden Markov Models-description
- S2: Hidden Markov Models-Lecture Slides version1
- S3. Hidden Markov Models-Additional notes for Introductory Lecture, version 1
- S4: Hidden Markov Models-Lecture Slides version 2
- S5: Hidden Markov Models-Student Manual
- S6: Hidden Markov Models-Spreadsheet for 5’ Splice Site Prediction
- S7: Hidden Markov Models-Homework
- S8. Hidden Markov Models-Additional references
- S9. Hidden Markov Models-HMM examples
- S10. Hidden Markov Models-Suggested manipulations for the Spreadsheet
ACKNOWLEDGMENTS
We would like to acknowledge and thank the students enrolled in the spring 2014 version of Bio 4342, Research Explorations in Genomics (Washington University), and the fall 2013 version of BIOL/CS 370, Introduction to Bioinformatics (Truman State University) for their contributions to assessment and feedback on this lesson. We would also like to thank members of Washington University Educational Research Group and the Elgin lab members for stimulating discussions. This work was supported by a Freiberg Visiting Fellowship for AW from Washington University, grant #52007051 from the Howard Hughes Medical Institute (HHMI) Precollege and Undergraduate Science Education Professors Program to Washington University (for SCRE), and IUSE grant #1431407 from the National Science Foundation to Washington University (for SCRE).
References
- Shaffer CD, Alvarez C, Bailey C, et al. 2010. The genomics education partnership: successful integration of research into laboratory classes at a diverse group of undergraduate institutions. CBE Life Sci Educ. Spring;9(1):55-69.
- Shaffer CD, Alvarez CJ, Bednarski AE, et al. 2014. A course-based research experience: how benefits change with increased investment in instructional time. CBE Life Sci Educ. Spring;13(1):111-30
- Eddy SR. What is Hidden Markov Model? 2004. Nat Biotechnol. Oct;22(10):1315-6
- Bykova NA, Favorov AV, Mironov AA. 2013. Hidden Markov Models for Evolution and Comparative Genomics Analysis. PLoS ONE 8(6):e65012.
Article Files
Login to access supporting documents
A Hands-on Introduction to Hidden Markov Models(PDF | 643 KB)
S1.Hidden Markov Models-description.pdf(PDF | 189 KB)
S2.Hidden Markov Models-Lecture Slides version1.pptx(PPTX | 128 KB)
S3.Hidden Markov Models-Additional notes for Introductory Lecture version 1.docx(DOCX | 148 KB)
S4.Hidden Markov Models-Lecture Slides version 2 .pptx(PPTX | 670 KB)
S5.Hidden Markov Models-Student Manual .doc(DOC | 208 KB)
S6.Hidden Markov Models-Spreadsheet for 5 Splice Site Prediction.xls(XLS | 565 KB)
S7.Hidden Markov Models-Homework Key AEW.docx(DOCX | 69 KB)
S8.Hidden Markov Models-Additional references .docx(DOCX | 131 KB)
S9.Hidden Markov Models-HMM examples.pptx(PPTX | 494 KB)
S10.Hidden Markov Models-Suggested manipulations for the Spreadsheet .docx(DOCX | 668 KB)
- License terms

Comments
Comments
There are no comments on this resource.