Learning to Pipet Correctly by Pipetting Incorrectly?
Published online:
Abstract
Beginning undergraduate students in biology need basic laboratory, data analysis, and science process skills to pursue more complex questions in course-based undergraduate research experiences (CUREs). To this end, we designed an introductory lesson that helps students learn to use common laboratory equipment such as analytical balances and micropipettes, analyze and present data in Google and Microsoft spreadsheet software, and perform simple descriptive and inferential statistics for hypothesis testing. In this lesson, students first learn to use micropipettes by pipetting specific volumes of water correctly and incorrectly. After determining the masses of the water samples pipetted, students enter the data into a shared Google spreadsheet and then use statistics to test a null hypothesis; ultimately, they determine if there is a statistically significant difference between the mass of water pipetted correctly versus incorrectly. Together, these activities introduce students to important data analysis and science process skills while also orienting them to basic laboratory equipment.
Citation
Mel, S.F., Micou, M.K., Gaur, K., Lenh, D., Liu, C.Z., and Lo, S.M. 2019. Learning to Pipet Correctly by Pipetting Incorrectly? CourseSource. https://doi.org/10.24918/cs.2019.7Society Learning Goals
Science Process Skills
- Process of Science
- Interpret, evaluate, and draw conclusions from data
- Construct explanations and make evidence-based arguments about the natural world
- Modeling/ Developing and Using Models
- Build and evaluate models of biological systems
- Quantitative Reasoning/ Using Mathematics and Computational Thinking
- Apply the tools of graphing, statistics, and data science to analyze biological data
- Communication and Collaboration
- Share ideas, data, and findings with others clearly and accurately
Lesson Learning Goals
- Students will become familiar with common laboratory equipment.
- Students will learn to analyze and present data.
- Students will understand the role of basic statistics in hypothesis testing.
- Students will construct scientific arguments.
Lesson Learning Objectives
- Students will be able to use analytical balances and micropipettes.
- Students will be able to calculate averages and standard deviations.
- Students will be able to use t-tests to compare two independent samples.
- Students will be able to justify accepting or rejecting a null hypothesis based on an interpretation of p-values.
- Students will learn to use spreadsheet software such as Microsoft Excel and/or Google Sheets
- Students will be able to explain how pipetting incorrectly leads to errors.
Article Context
Course
Article Type
Course Level
Bloom's Cognitive Level
Vision and Change Core Competencies
Class Type
Class Size
Audience
Lesson Length
Pedagogical Approaches
Principles of How People Learn
Assessment Type
INTRODUCTION
All first-year undergraduates majoring in biological sciences at our institution are required to take an introductory laboratory course that is designed as an ongoing research project on soil microbiomes (1). These students typically have little to no laboratory experience, although many will go on to work in faculty research groups. Throughout this course, students use micropipettes and spreadsheet software to collect and analyze data. Because the data generated in this course are novel, we wanted to ensure that students are comfortable with both pipetting and spreadsheet software before they start working with the actual soil samples used for microbiome analysis. While others have published excellent pipetting activities with different emphases (2-5), this lesson adds a new dimension by providing students with the opportunity to validate their pipetting technique using statistical analyses, in addition to teaching them how to pipet correctly. An abbreviated version of this lesson was previously presented as a mini-workshop at the Association for Biology Laboratory Education meeting (6).
INTENDED AUDIENCE
Currently, the lesson is implemented in an introductory biology laboratory course for first-year undergraduates in biological sciences at a large public doctoral university (highest research activity and high undergraduate enrollment profile) (Carnegie Classification) (7). In our setting, the lesson is taught by graduate and undergraduate instructional assistants in a laboratory classroom with 24-32 students, who work in teams of up to four students. We envision that the lesson can potentially be used at the high school, college, or university level.
REQUIRED LEARNING TIME
The lesson is carried out in one three-hour laboratory period, and the activities take approximately two hours (Table 1).

Table 1. Learning How to Pipet - Teaching Timeline
PRE-REQUISITE STUDENT KNOWLEDGE
The lesson is designed for students with minimal background in biology and little to no laboratory experience. Additionally, students do not need any previous experience in statistics or spreadsheet software. As a pre-laboratory assignment, we ask students to complete tutorials 1-4 of the Spreadsheet Data Analysis Tutorials from HHMI BioInteractive, which introduce basic spreadsheet skills and statistical tests (https://www.hhmi.org/biointeractive/statistics-and-math), and to read a short review on hypothesis testing (8).
PRE-REQUISITE TEACHER KNOWLEDGE
For the laboratory portion of the lesson, the instructor should know how to use analytical balances and micropipettes. For the data analysis and presentation portion, the instructor should be familiar with how to carry out basic mathematical operations, calculate means and standard deviations, and perform t-tests in Microsoft Excel and/or Google Sheets. The instructor should also know how to generate graphs in these software programs. Finally, the instructor should be familiar with the structure of a scientific argument, including the claim, evidence, and justification (9-11).
SCIENTIFIC TEACHING THEMES
ACTIVE LEARNING
Students collaborate in small teams to carry out the lesson and analyze data collected by different teams in the course. Here, we use the interactive, constructive, active, and passive (ICAP) framework to define the various active-learning activities in the lesson (12-13). First, student teams actively manipulate laboratory equipment to collect data for further analysis ("active" in ICAP). Then, students analyze the data collected by all the teams in the laboratory section, and they generate graphs to represent these data through interactive dialogs within and across teams ("interactive" in ICAP). Finally, individual students construct a scientific argument and generate an explanation for how to pipet correctly ("constructive" in ICAP).
The lesson is designed to teach students how to use micropipettes correctly and to challenge potential misconceptions that students with pipetting experience may have, e.g. they should use the second stop on the micropipette to draw up solutions. Students are first asked to pipet correctly by drawing up water from the first stop of the micropipette and then releasing the water using the second stop. Next students are asked to pipet incorrectly by drawing up water from the second stop, which results in inaccurate and larger volumes, and then releasing the water also using the second stop. Students then compare the masses of water transferred by the correct versus incorrect methods of pipetting, and they determine whether the two different methods result in statistically significant different outcomes. This comparison enables students to use quantitative methods to address their potential misconception.
ASSESSMENT
This lesson includes both formative and summative assessments (14-15). First, as a formative assessment, all student teams enter their data from pipetting correctly and incorrectly into a shared Google spreadsheet while still in the laboratory. The shared data provide students the opportunity to assess their results in the context of the data generated by all teams in the laboratory section. By comparing their data with those from other teams, students can determine if they have made errors in pipetting; they can then re-do the measurement and correct the error. Further, instructors and instructional assistants can identify problems on the spot and then can initiate discussions to help students identify the source of the problem. Second, as a summative assessment, individual students construct a scientific argument using the pipetting results from the entire class. For this assignment, students generate a graph of the results, create a figure caption, summarize and analyze the data, draw a conclusion from the data, and explain why pipetting using the second stop results in a statistically larger quantity of water.
INCLUSIVE TEACHING
This lesson assumes no prior knowledge and is thus inclusive of students with different experiences. Students also work in teams, which provides opportunities for sharing existing expertise. For example, some students may have used micropipettes in the past, while others may have done data analysis and statistics in spreadsheet software. Even though students self-select to form teams, we have found based on our observations that most teams typically consist of diverse expertise. Team members are strongly encouraged to rotate tasks, so that everyone can experience and learn the different tasks within the lesson. In our experience, we find that when students form their own teams, they are comfortable working with one another, consistent with research showing that self-selected teams have better communication, are more enthusiastic about working together, take interest in one another, feel more confident in the other teammates' abilities, and are more productive and equitable (16).
LESSON PLAN
PRE-CLASS PREPARATION
Each student team has a set of micropipettes (P10, P100, and P1000). From this set, they select the appropriate micropipette to use for each volume they need to pipet. Students are also given a supply of pipette tips, both small and large, and empty 1.5-mL microtubes. The mass of the microtubes with and without water is determined on an analytical balance. Any brand of air displacement micropipette, microtube, and analytical balance will work.
IN-CLASS SCRIPT: PIPETTING
The lesson begins with a discussion about the importance of pipetting correctly for experiments to be successful. The instructional assistants demonstrate the use of micropipettes, emphasizing the difference between depressing to the first stop of the micropipette, which draws up the correct volume, and depressing to the second stop, which draws up a larger and incorrect volume, and highlighting that the second stop is used to release the full volume of the pipetted solution because of surface tension. In addition, the instructional assistants point out that if a volume can be transferred with more than one of their micropipettes, students should use the one with the lower volume range for increased accuracy.
The volumes pipetted and the number of samples analyzed for each volume pipetted are up to the discretion of the instructor. A summary of the steps in the order that we typically use in this lesson is listed below. A sample data set is shown in Figure 1.
- Record mass of individual, empty 1.5-mL microtubes on a shared Google spreadsheet.
- Pipet a selected volume of water correctly into each microtube by depressing to the first stop on the micropipette. In our laboratory, we use 60 μL for this volume.
- Pipet the same selected volume of water incorrectly into microtubes by depressing to the second stop on the micropipette.
- Pipet a second selected volume of water correctly into tubes. In our laboratory, we use 120 μL for this volume.
- Pipet the same selected volume of water incorrectly into microtubes.
- Record mass of microtubes plus water on a shared Google spreadsheet.
It is important that each student pipets at least one correct and incorrect sample each, to understand the difference. For example, in our laboratory, each team has four students: Student A pipets 60 μL correctly and 60 μL incorrectly; student B does the same; students C and D each pipet 120 μL correctly and 120 μL incorrectly. In this way, each sample is run in duplicate.
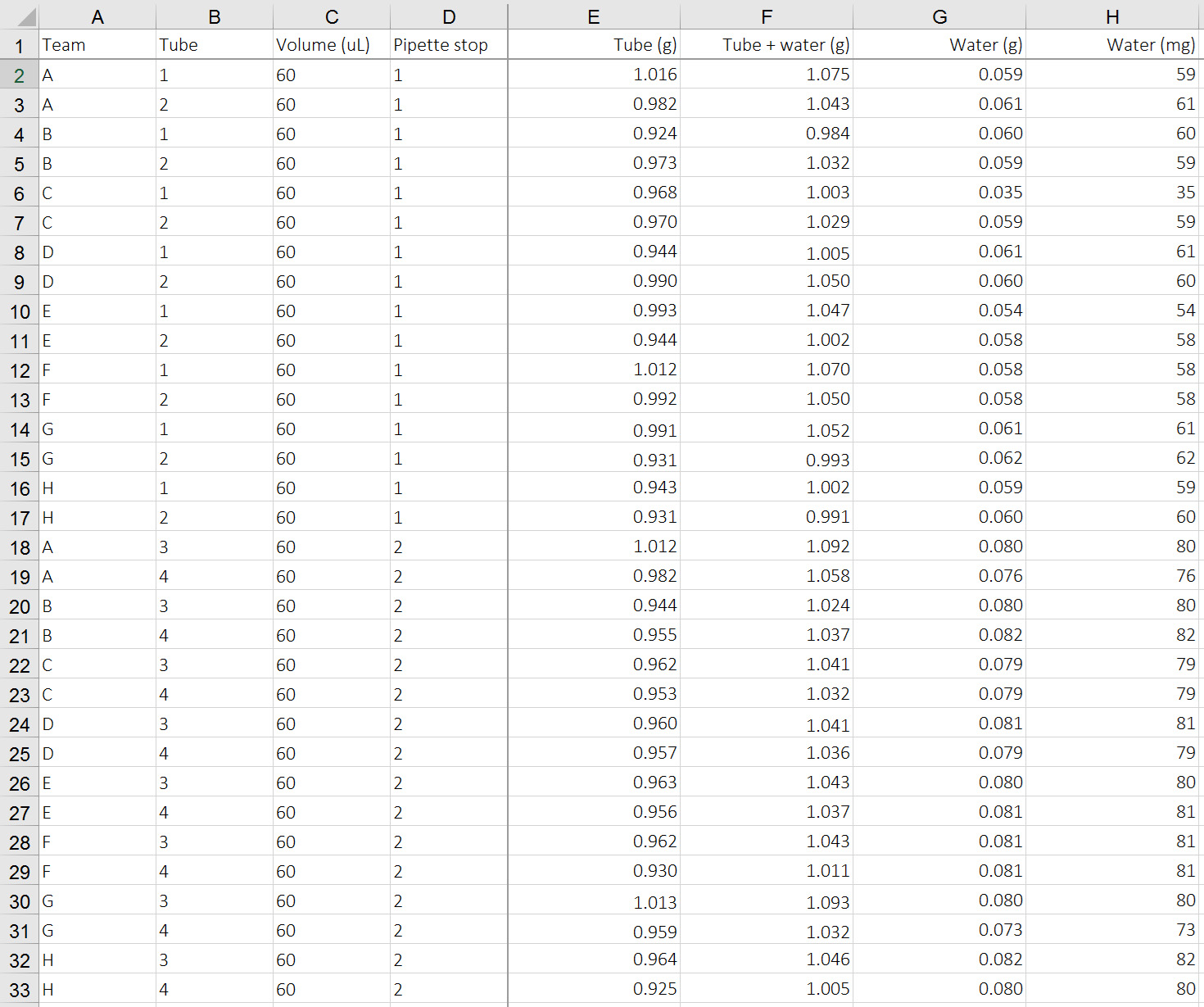
Figure 1. Sample data collected by student teams A-H (Column A) from one laboratory section. Each team ran duplicate samples for each volume pipetted both correctly and incorrectly (Columns B-D): Tubes 1 and 2 = 60 µl pipetted correctly, Tubes 3 and 4 = 60 µl pipetted incorrectly, Tubes 5 and 6 = 120 µl pipetted correctly, and Tubes 7 and 8 = 120 µl pipetted incorrectly. The mass of the water pipetted was calculated using standard functions in Excel (Columns E–H).
IN-CLASS SCRIPT: DATA ANALYSIS
DETERMINING MASS OF WATER
The shared Google spreadsheet allows different teams of students to enter data simultaneously. In our laboratory, we then ask students to download the Google spreadsheet and perform the calculations individually in Microsoft Excel, so that everyone is responsible for their own work and has the opportunity to practice data analysis.
Students first calculate the mass of water in each tube by subtracting the mass of each tube alone from the mass of the tube with water using the minus ("-") calculation. For example, students type =(F2-E2) into cell G2 to determine the mass of the water pipetted by Team A in Tube 1 (Figure 1). To determine the mass of water in milligrams instead of grams, students use the multiply ("*") or divide ("/") calculation as appropriate.
CALCULATING AVERAGE AND STANDARD DEVIATION
The next part of the lesson begins with a discussion about how students will analyze the results of pipetting correctly vs. incorrectly. Students first calculate averages and standard deviations for each of the data sets (i.e. 60 μL correctly, 60 μL incorrectly, 120 μL correctly, and 120 μL incorrectly) and then perform t-tests to determine if pipetting correctly vs. incorrectly leads to a statistically significantly different result.
The instructional assistants demonstrate how to use the =AVERAGE() and =STDEV() functions to calculate average and standard deviation. Students then calculate these values for each of the correctly and incorrectly pipetted volumes. The syntax for calculating an average is =AVERAGE(first cell containing data:last cell containing data). For example, =AVERAGE(H2:H17) calculates the average of all values in cells H2 to H17, which represents the average of the correctly pipetted 60-μLvolumes (Figure 1). The analogous calculation can be done for standard deviation using the formula =STDEV(). See Table 2 for a summary of the averages and standard deviations for a sample set of this data.

Table 2. Learning to Pipet - Statistical analysis of data from one laboratory section of up to 32 students in eight teams, with n = 16 for each combination of volume and pipette stop. Pair-wise comparisons between the correct and incorrect pipetting methods have p < 0.0001 as determined by two-tailed t-tests.
CALCULATING A P-VALUE FROM A T-TEST
Students use a t-test to determine if there is a statistically significant difference between the correctly and incorrectly pipetted volumes. The result of the t-test will be a p-value, which indicates the probability that the two samples have come from the same population. A common (but arbitrary) threshold is p<0.05, which would mean there is less than a 5% chance that the correctly pipetted volume is the same as the incorrectly pipetted volume. In this case, students could conclude that the volumes are significantly different. Importantly, during the discussion, the instructor asks students to think about how this result would validate the importance of using the correct pipetting technique.
To calculate a p-value, students use the Excel formula =TTEST(array1,array2,2,3), where the two arrays are the cell ranges containing the two data sets. For example, to determine if correctly and incorrectly pipetted 60 μL volumes are the same or different, students would use the following formula: =TTEST(H2:H17,H18:H33,2,3). The "2" in the formula refers to the fact that we use a two-tailed t-test, which does not make any assumptions about which pipetting method (correct or incorrect) leads to larger measurements. Note that this part of the lesson would be an opportunity to have a discussion with students about the difference between one- and two-tailed t-tests. The "3" in the formula indicates that our samples are unpaired and do not have the same variance. Sample p-values from our class data are listed in Table 2.
TEACHING DISCUSSION
INSTRUCTOR OBSERVATIONS
The following observations suggest that most students achieve the learning outcomes of this lesson. First, data collected by students (and instructional assistants as a comparison group) are highly consistently and accurate (Figure 2) and indicate that students pipetted and measured the samples correctly. Second, as a writing assignment (rubric available by request), each student constructs their own scientific argument and demonstrates that they can perform calculations and statistical analysis on the data and understand the principle of pipetting correctly by drawing up solutions using the first stop on micropipettes. Finally, the introduction of this lesson into our CURE (1) has led to more consistent results in the subsequent experiments, e.g. setting up 96-well plates with equal volumes of samples in each well.
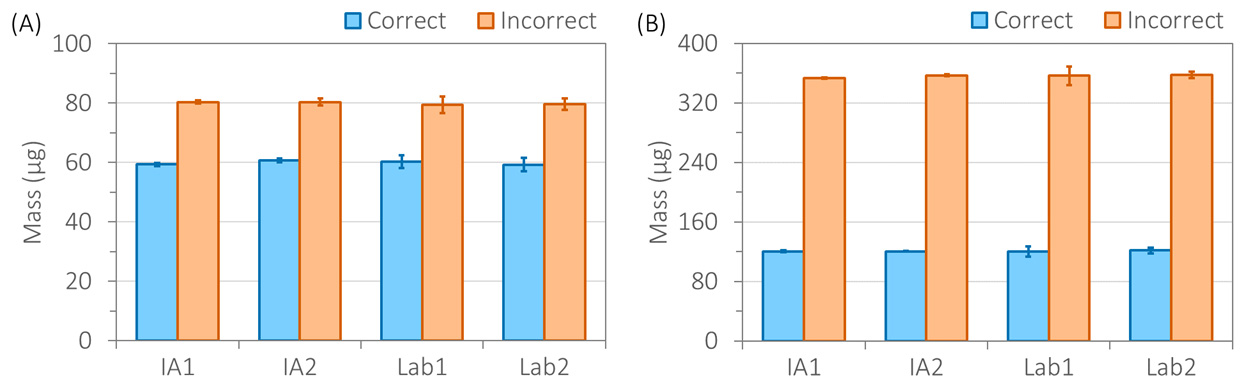
Figure 2. Sample data collected for 60-μL samples (A) and 120-μL samples (B) by individual instructional assistants (IA1 and IA2), who are experienced in pipetting, and students in laboratory sections (Lab1 and Lab2). In an ANOVA with the Tukey-Kramer HSD method, each corresponding pair of volumes pipetted by IAs and students show no statistical difference. In addition, all pair-wise comparisons between the correct and incorrect pipetting methods have p < 0.0001.
STUDENT REACTIONS
We find that our students react positively to this lesson, despite the fact that pipetting correctly vs. incorrectly is not addressing an inherently interesting biological question. Students are excited by the very small p-values that are typical of our results, and this helps them understand the importance of pipetting correctly.
POSSIBLE ADAPTATIONS
This lesson introduces students to basic laboratory, data analysis, and science process skills and thus should be widely adaptable to introductory laboratory courses at different institutional levels. We acknowledge that analytical balances may be a limiting resource, and the lesson could be modified to use large volumes and normal balances. In our case, students continue to use analytical balances throughout the microbiome research project (1), so the equipment is an investment for the entire course beyond this lesson.
We previously had a variation of this lesson in which students calculate the percent error of the mass of water that they pipet. We found that doing two calculations (percent error and t-test) was too much for a three-hour laboratory period, so we opted to focus on the statistical analysis instead. In addition, the percent error for the correct method measures the inherent variations of pipetting, whereas the percent error for the incorrect method contains both the additional volume from using the second stop to draw up solutions and the inherent variations of pipetting. This finer point complicates the discussion on errors, and we were not able to explore it fully with our students due to the limited time of this lesson.
For the statistical analysis, we opted to perform a simple t-test to compare the means of pipetting correctly vs. incorrectly for each volume, as this is an introductory course intended for first-year undergraduates who are not likely to have taken the required statistics course in our curriculum. Depending on the level of the course, instructors at other institutions can use this lesson as an opportunity to introduce students to ANOVA, where the independent variables are volume (60 μL or 120 μL) and method (correct or incorrect).
In the past, we also did an iteration of this lesson in which a flaw in experimental design was intentionally introduced into the protocol. Students measured the total mass of 12 microtubes and calculated an average mass for each microtube. The inherent variation in the mass of microtubes (Table 3) is typically in the range of the mass for 60 μL of water, thus canceling out the effect of pipetting correctly vs. incorrectly. While this iteration provided an opportunity to discuss potential sources of errors beyond human mistakes and instrumental inaccuracies, we found that students struggled with the idea of being given incorrect protocols in the laboratory. Furthermore, the follow-up discussions on sources of errors could be quite variable depending on the scientific experience and pedagogical skills of individual instructional assistants. It is conceivable that much more productive discussions and outcomes would be possible in smaller courses where the instructor is present the whole time and directly leads the lesson.
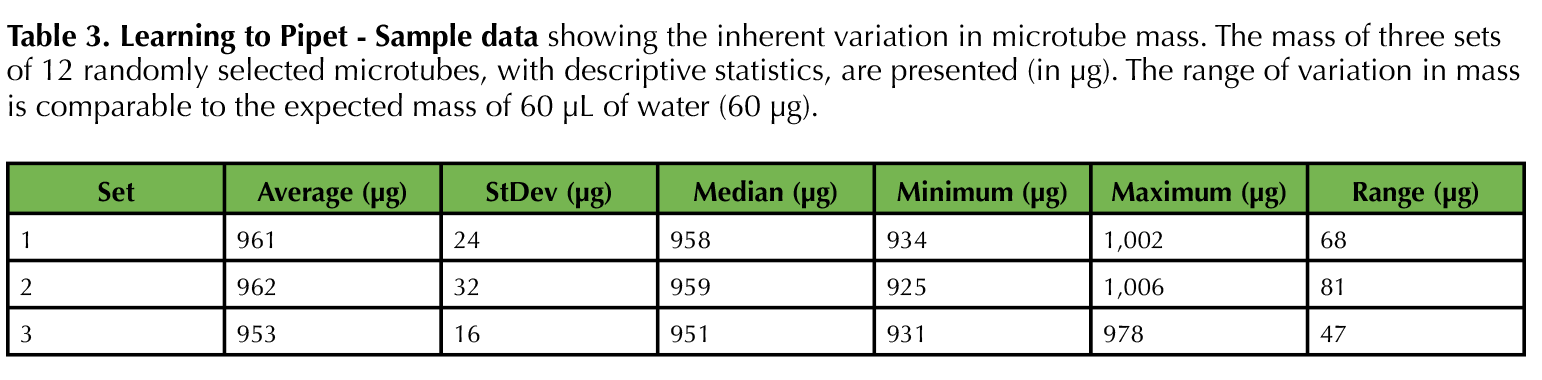
Table 3. Learning to Pipet - Sample data showing the inherent variation in microtube mass. The mass of three sets of 12 randomly selected microtubes, with descriptive statistics, are presented (in µg). The range of variation in mass is comparable to the expected mass of 60 µL of water (60 µg).
ACKNOWLEDGMENTS
We are grateful to all the students, instructional assistants, laboratory staff, and faculty members who have participated and contributed to the implementation of this lesson. This work was supported in part by the Teaching Professor Summer Research Fellowship Program (awarded to SFM) in the Division of Biological Sciences at University of California San Diego.
References
- Lo SM, Mel SF. 2017. Examining microbial biodiversity in soil: A large-enrollment introductory course-based undergraduate research experience. Tested Studies in Laboratory Education 38: 6.
- Burnette JM, Kanizay L, Chester N, Wessler SR. 2016. Dilution and pipetting lesson using food dyes. CourseSource. https://doi.org/10.24918/cs.2016.5
- Guzman K. 2001. Pipetting: A practical guide. American Biology Teacher 63: 128-131.
- Miller J, Sass ME, Wong SJ, Nienhuis J. 2004. Micropipetting: An important laboratory skill of molecular biology. The American Biology Teacher 66: 291-296.
- Moni RW, Hryciw P, Poronnik P, Lluka LJ, Moni KB. 2007. Assessing core manipulative skills in a large, first-year laboratory. Advances in Physiology Education 31: 266-269.
- Mel SF, Lo SM. 2018. No, It's Not About Pipetting! Tested Studies for Laboratory Teaching: Proceedings of the Association for Biology Laboratory Education 39: Article 41.
- McCormick AC, Zhao C-M. 2005. Rethinking and reframing the Carnegie Classification. Change: The Magazine of Higher Learning 37: 51-57.
- Whitley E, Ball J. 2002. Statistics review 3: Hypothesis testing and P values. Critical Care 6: 222-225.
- Chen Y-C, Steenhoek J. 2014. Arguing like a scientist: Engaging students in core scientific practices. The American Biology Teacher 76: 231-237.
- Sampson V, Clark DB. 2008. Assessment of the ways students generate arguments in science education: Current perspectives and recommendations for future directions. Science Education 92: 447-472.
- Sampson V, Schleigh S. 2013. Scientific Argumentation in Biology: 30 Classroom Activities. Arlington, VA: NSTA Press.
- Chi MTH. 2009. Active-constructive-interactive: A conceptual framework for differentiating learning activities. Topics in Cognitive Science 1: 73-105.
- Chi MTH, Wylie R. 2014. The ICAP framework: Linking cognitive engagement to active learning outcomes. Educational Psychologist 49: 214-243.
- Dirks C, Wenderoth MP, Withers M. 2014. Assessment in the College Science Classroom. New York, NY: W.H. Freeman.
- Handelsman J, Miller S, Pfund C. 2006. Scientific Teaching. New York, NY: W.H. Freeman.
- Chapman KJ, Meuter M, Toy D, Wright L. 2006. Can't we pick our own groups? The influence of group selection method on group dynamics and outcomes. Journal of Management Education 30: 557-569.
Article Files
Login to access supporting documents

Comments
Comments
There are no comments on this resource.