Quantifying Uncertainty and Distinguishing Data Sets in Introductory Physics
Editor: Jenny Knight
Published online:
Abstract
Physics labs are moving increasingly to open-ended experiments where students develop experimental physics skills, rather than verify textbook physics concepts. This sequence of activities sets the stage for this new kind of lab early in the semester, while introducing key skills and concepts related to uncertainty, data analysis, and interpreting results in light of uncertainty. The activities also prepare students for successful collaboration throughout the semester, focusing particularly on how to distribute or share productive team roles. The sequence of activities centers on measurements of the angle dependence of a period of a pendulum—a relatively quick experiment that allows students to design and implement multiple measurement approaches to reduce uncertainty. Ultimately, students’ results depend on the precision with which they can make the measurement, facilitating conversations about the nature of science and measurement alongside issues of ethics and what it means to engage in authentic scientific practice.
Primary Image: A generic histogram.
Citation
Scherr RE, Holmes NG. 2023. Quantifying Uncertainty and Distinguishing Data Sets in Introductory Physics. CourseSource 10. https://doi.org/10.24918/cs.2023.44Lesson Learning Goals
Students will:- understand sources of uncertainty in measurement and the importance of reducing uncertainty.
- value the role of uncertainty in making comparisons between measurements.
- connect the activities in the lab to authentic scientific practice and their everyday lives.
- understand the importance of working collaboratively.
Lesson Learning Objectives
Students will be able to:- generate, discuss, and reflect on a team agreement, including how to distribute or share a range of productive team roles.
- generate a histogram of repeated measurements.
- calculate statistical uncertainty associated with a measurement or set of measurements using standard deviation and standard uncertainty, as appropriate.
- identify and distinguish sources of uncertainty and sources of human errors (mistakes) and use them to find and implement methods for reducing uncertainty.
- articulate the benefits of measuring multiple consecutive periods in terms of the sources of uncertainty.
- quantitatively compare pairs of measurements using differences in units of uncertainty and interpret the comparisons using appropriate argumentation practices, including multiple, reasonable, and possible interpretations.
Article Context
Course
Article Type
Course Level
Bloom's Cognitive Level
Vision and Change Core Competencies
Class Type
Class Size
Audience
Lesson Length
Principles of How People Learn
Assessment Type
Introduction
Nationally, physics laboratory instruction is shifting away from traditional, model-verifying activities that aim to reinforce content, toward open-ended investigations that engage students in the practices of scientific experimentation (1–4).
We present a three-session sequence of lab activities in which students emulate the activities of professional physicists, including testing models with appropriate data collection methods, refining and iterating an experimental design, and deciding how to evaluate models using experimental data (Table 1). This three-session sequence is part of a year-long curriculum emphasizing experimental science skills.
Table 1. Teaching timetable.
| Activity | Description | Estimated Time | Notes |
|---|---|---|---|
| Week 1: Measuring Uncertainty | |||
| Opening activity |
Intro to lab Pendulum demo data collection |
30 min | Supporting Files S1–3 |
| Teamwork | Quantify uncertainty | 90 min | Supporting Files S4–6 |
| Follow-up question | Reflect on learning goals | 10 min | Supporting File S7 |
| Week 2: Reducing Uncertainty | |||
| Opening discussion | Distinguishing data sets: why it matters, invent quantification | 30 min | Supporting File S8 |
| Teamwork | Reduce uncertainty | 90 min | Supporting Files S9 and S10 |
| Follow-up question | Propose data sets that matter to you, critique experiment | 20 min | Supporting File S11 |
| Week 3: Comparing Data Sets | |||
| Opening discussion | Distinguishing real data sets in education and physics, calculating t-prime | 30 min | Supporting File S12 |
| Teamwork | Calculating distinguishability, further reducing uncertainty, answering experimental question | 90 min | Supporting Files S13 and S14 |
| Follow-up question | Scientific integrity | 10 min | Supporting File S15 |
This sequence particularly focuses on the role of uncertainty in measurement, both from a conceptual and quantitative perspective. The sequence is set within the context of a period of a pendulum measurement, whereby students test whether the amplitude of the pendulum affects its period. In many introductory physics courses, students are presented with (and often derive) an equation that indicates that the period is independent of the amplitude, depending only on the length of the pendulum (L) and fundamental constants (, acceleration due to gravity): . The derivation of this equation, however, involves an approximation that assumes that the angle of amplitude of the pendulum is small; that is, that: . In this sequence, as students iteratively design experimental procedures with improved precision, they may be able to distinguish periods from two different amplitudes.
Quantitatively, the sequence introduces students to mathematical ways to calculate the uncertainty of their measurement of the period of the pendulum. They are first introduced to the standard deviation and standard uncertainty of the mean, with lessons that conceptually connect the mathematical formulations to the conceptual understanding of variability between repeated measurements. The sequence also has students explore the impact of measuring the time for multiple periods of the pendulum at once (e.g., starting the stopwatch and measuring the time for periods) as another way to reduce uncertainty beyond taking additional repeated measurements. Finally, the sequence also introduces students to a quantitative way to distinguish two measurements as a fraction of the uncertainty in those measurements. Versions of this sequence have been analyzed in other work (1–3, 5–7) and this adapted version responds to those research results in several ways, which we articulate in the Scientific Teaching Themes section.
Intended Audience
This lesson is intended for students taking their first college-level physics course. It was specifically adapted for students with relatively little physics background and is appropriate for algebra-based or calculus-based physics, instructed by faculty or graduate teaching assistants.
Required Learning Time
This lesson sequence is designed to span three two-hour lab periods, including short (<20 minutes) reflection activities for homework.
Prerequisite Student Knowledge
There is no physics-specific prerequisite student knowledge for this lesson. Students will benefit from having basic skills for using electronic spreadsheets to do calculations and create charts.
Prerequisite Teacher Knowledge
Instructors should be familiar with calculating and interpreting standard deviation and standard uncertainty in the mean. Instructors should have basic skills for using electronic spreadsheets to do calculations and create charts. They should also know the key features of a histogram, including what distinguishes a histogram from a bar chart. Although we expect that physics instructors know about the small-angle approximation for the period of a pendulum, that knowledge is not needed for effective laboratory instruction.
Scientific Teaching Themes
Active Learning
While labs may be considered inherently “active” in that students handle equipment, the activities in this lesson are intentionally designed to support active engagement with experimental physics concepts and practices.
A key goal in the shift towards engaging students in the practices of scientific experimentation is to support student agency by encouraging and supporting students to do more of the decision-making in the experiment (8–12). This increased freedom must also be balanced with structure to support their learning; it’s not that “anything goes”—students still must learn to make decisions that are in line with scientific practice and argumentation. Thus, the activities strike a fine balance between structure and agency. On the structure side, each session clearly articulates how students will be assessed, which decisions they ought to make and justify, and ways to have productive teamwork. On the agency side, each session leaves room for students to make choices and their own decisions. For example, rather than telling students to require 10 consecutive periods of the pendulum for each measurement, the instructions ask students to reflect on the impact of measuring consecutive periods on the precision of their measurement, identify additional methods to reduce uncertainty, and choose one method and implement it.
A second key goal in the shift is towards open-ended investigations (3, 6, 11, 13). Here, we define open-ended as meaning that the result of the experiment is not known prior to doing the experiment. In the first two sessions, the role of the small angle approximation in the measurements is known to the instructor, but rarely known to the students. In our experience, even if students know about the approximation, they do not know whether it is measurable or whether the angles 10° and 20° are “small enough.” Different student groups will likely come to different conclusions, particularly depending on the precision with which they measure the period.
For many students, the question of whether the measurements of the period from 10° and 20° will be distinguishable is an entirely open question: they have no strong expectations and accept the question as experimental. Other students, having learned that the period of a pendulum is independent of amplitude (for small angles), are very surprised to find that the measurements are distinguishable. Previous research evaluating a version of this activity found that moderate proportions of students exhibit questionable research practices associated with confirming the canonical theory (that the amplitude will not affect the period), such as discarding data that does not fit their expectations (6, 14, 15). The finding that the period can depend on amplitude often directly confronts students’ expectations for lab because the goal is not to demonstrate or apply concepts from the textbook. This confrontation is intentional to help shift students’ expectations for what will happen in the rest of the semester.
Lastly, the activities also include a form of active learning known as “Invention Activities” (16, 17). In an invention activity, students are given carefully designed contrasting cases that set up an open-ended problem to be solved. Students then invent solutions to the problem, prior to receiving instruction on canonical strategies. In this activity, students invent a way to quantify distinguishability from four contrasting cases of pairs of measurements with different means, standard deviations, and standard uncertainties in the mean. The contrasting cases are deliberately set up to engage students with relevant features of the problem, which will need to be accounted for in their invention. Invention activities have been shown to improve students’ conceptual understanding of the associated target concept and improve students’ performance on subsequent transfer tasks (18–20). Students are given about 10 minutes to invent in their groups, working on whiteboards to support creativity and collaboration. The instructor then leads a discussion that highlights the contrasting features, presents examples of the range of student inventions, and ultimately pulls the ideas together to present the canonical solution. Students need not invent a correct solution or even generate a complete solution; they need only engage constructively with the cases and grapple with the relevant features.
Assessment
Students are assessed through three means:
-
“Lab Practices,” graded according to a participation rubric (Supporting File S1). The Lab practices assessment is a form of formative assessment, whereby the students get immediate feedback from the instructor during the check-in.
-
“Lab Notebook,” a group submission at the end of lab, graded according to rubrics provided each session. The Lab Notebook assessment is simultaneously formative and summative, as a way to evaluate their progress towards the intended scientific practices (21).
-
“Lab Follow-Up Questions,” answered individually a few days after each lab session and graded for completion. The Lab Follow-Up Questions support self-assessment and reflection, and offer assessment at the individual level.
Inclusive Teaching
Inclusive teaching is addressed with group size, brief teambuilding activities, and intentionality and reflection about team roles.
Group Size
We use groups of 2–3 students, not 4 or more. This ensures that there are enough students to tackle all the tasks and to effectively brainstorm, but not so many students that individuals do not participate. We give them an icebreaker on the first day to get to know each other.
Roles
We introduce team roles by offering a handout describing various scientific roles (Supporting File S2), articulating that these are all tasks that need doing in science. We typically introduce the following roles as possibilities: Equity Monitor, Principal Investigator, Science Communicator, Data Analyst, Skeptic, and Theorist. We tell students they have freedom to decide how to accomplish these things, but require them to make an intentional choice. Not all the roles are important for every investigation, and because there are only 2–3 students, they may need each person to have more than one role. We give students time to discuss and make a Team Agreement, which is recorded in their lab notebook. Later, if teams fall short in some way, we refer to their roles when giving lab notebook feedback: for example, “Make sure you assign a skeptic next time so you can catch errors like this one” or for an off-task group, “Who’s the PI?” Students are prompted to reconsider their Team Agreement every lab. One of the lab follow-up questions asks students to reflect on the roles they have taken in their teams; what comes naturally to them, and what do they want to work on?
Lesson Plan
Experimental Context
In this three-week lab investigation, students decide whether the period of a pendulum released from 10° is different from that of a pendulum released from 20°. Although the textbook says that the period of a pendulum is independent of amplitude, this is an approximation for small angles; whether the periods are different for 10° and 20° is an experimental question.
Documenting Investigations
Students document their investigations in an editable electronic document (such as a Google Doc) shared with all members of the team and the instructor. The document is for continuous, comprehensive documentation of lab equipment, methods, activities, data, decisions, and conclusions, and includes not only text but also drawings, photographs, graphs, and so on; it is not a formal lab report. To easily distinguish student contributions, each student uses a different font color. Instructors provide feedback in the form of (a) comments on the editable document and (b) scoring via a rubric specific to each session (see below).
Session 1. Measuring Uncertainty
In the first session, students observe as the instructor releases a large pendulum at the center of the room, first from an angle of 10° and then from an angle of 20° (Supporting File S3). Angles are measured on a protractor mounted at the top of the pendulum. Each individual student is instructed to measure the period (the time for one single oscillation of the pendulum) with their own stopwatch. The instructor releases the pendulum silently, giving no instructions about exactly how to measure the period, and catches the pendulum after one or two swings: they may do this once for practice and once for the actual measurement. Each student writes the time they recorded on the board or in a shared document.
This initial exercise raises many issues about accurate measurement. For example, students may or may not be able to see the pendulum well, they have different reaction times, and they make different choices about when to begin and end their timing (e.g., at the top or bottom of the pendulum swing). The resulting student measurements of the period typically vary by multiple tenths of a second.
Instructions are provided directly to students for them to work in their small groups (Supporting File S4, S5), with intermittent instructor support. Students are invited to determine the precision (instrumental) uncertainty for their measurements of the period of the pendulum; create a data table for the class’s measurements of the period, for both 10° and 20°; create a histogram for each data set; calculate the mean and the statistical uncertainty (standard deviation) for each data set; observe which uncertainty is greater (precision or statistical); and express the measurement of the period of the pendulum at each release angle as , where is the mean (average) value and is the greater of the two uncertainties. Finally, and importantly for the next session, students are asked to reflect on the variation in measurements: why is there variation? If the variation is due to mistakes made in measurement, how can those be corrected? What are some specific, practical strategies for reducing the variation in the measurements?
In our classes, students may never have made a histogram. This is a valuable technical skill that they will use for the rest of this and other courses; students often report being happy to learn it. We suggest letting them use any program they prefer (Desmos, Excel, Google Sheets, etc.); the variability of approaches is instructive.
After each lab session, students submit lab notebooks to be scored according to a session-specific scoring rubric (Supporting File S6) and complete a brief follow-up assignment (Supporting File S7). The follow-up question for this first session invites students to reflect on the learning goals for the lab, which we expect they may find unusual. Students typically respond that these learning goals are very different from other labs, in which they have been expected to follow a specific protocol.
Session 2. Reducing Uncertainty
In the second session, students’ main task is to reduce the uncertainty in their measurements of the pendulum period. First, however, they engage in two opening discussions that add significance to their activity (Supporting File S8). The first short opening discussion is centered on the prompt: “Identify two sets of data that, if their similarity or dissimilarity were known, would have a noticeable impact on either your personal life or your community.” This prompt is inspired by our belief that the skills of distinguishing data sets are not only for the sake of succeeding in physics labs, but support informed decision making in many areas of life. For example, the first author (RES) shares the following questions that are essentially about distinguishing data sets: (a) Are medical outcomes different for people like her who, upon contracting COVID-19, take Paxlovid or don’t? (b) Are students more satisfied with her class if the class has undergraduate instructional assistants? (c) Does the frequency of hate crimes depend on who’s in a political office? Students are invited to discuss with their partners data sets that feel important to them.
The second short opening discussion is intended to help students begin to imagine quantifying the distinguishability of data sets. The instructor first introduces students to a histogram representation in which the mean is indicated with a dot, the standard deviation (σ) is a dashed line, and the standard uncertainty in the mean (δ) is a solid line. Students are then provided with four different histograms of repeated measurements of some quantity (Figure 1) and invited to discuss the following question in small groups: “On a scale of 1 (not confident) to 5 (very confident), how confident are you that the following students are measuring two different things? (i) students A and B, (ii) students A and C, (iii) students A and D.” In a whole-class discussion, instructors invite students to share the criteria that they used to say whether the data sets seem different to them. Students typically raise multiple useful ideas in this discussion, including the ideas that distinguishability is relative to both uncertainty and to the difference of the means, and that confidence increases with the number of data points. Instructors then ask students to invent different ways to quantify their confidence in the distinguishability of the four sets of measurements, in line with the above criteria. Instructors might say, for example, “One possible measure would be the difference of the means: the greater the difference, the more distinguishable the data sets. However, this doesn’t include everything you know is important. Try to come up with a formula that includes everything that you know matters.” Although most students struggle to invent a quantitative measure that embodies their sense of what is important, their effort helps prepare them to understand the quantitative measure they will use in the following session.
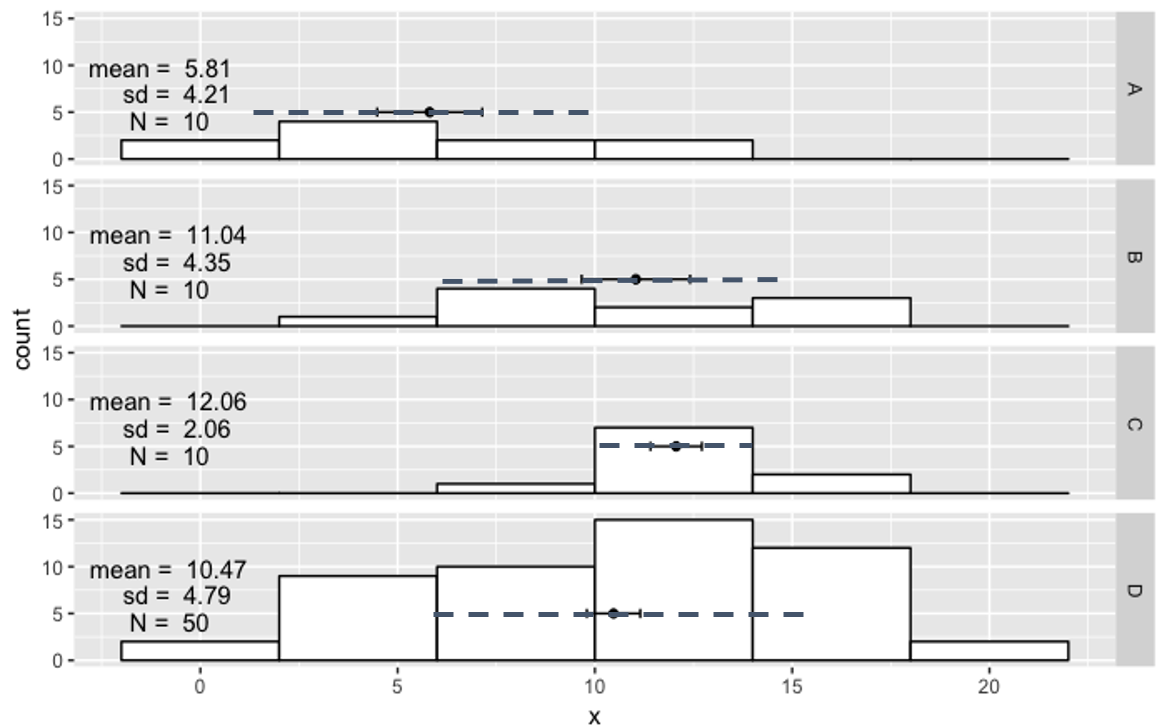
After recording their discussion and checking up on their team agreement, students spend most of the lab period working to reduce the uncertainty in their measurements of the pendulum period (Supporting File S9). Each student group has a pendulum at their lab table, typically a ring stand from which a plumb bob hangs by a thin string about 30 cm long, and a small protractor that students may tape to the pivot point. Questions prompt them to consider and reflect on the number of consecutive swings that they measure. For example, why would measuring multiple consecutive pendulum swings reduce the uncertainty of their value for one period compared to what they would obtain if they instead timed one period for five separate swings? Open-ended prompts motivate students to iteratively revise their measurement procedure with the goal of achieving a precision better than 0.01 s, which (we know from experience) is what may be needed to distinguish the data sets.
During their iterative redesign, students are encouraged to consult with other groups to learn about their approaches and ideas, recording with whom they consult so they can properly credit them later. In the second half of the session, instructors should provide a means for students to share the measurements that they are achieving (including standard deviation and uncertainty) so that they can compare results and catch any errors. Creating a table on the class whiteboard with a row for each group is one possible method.
Lab notebooks are scored with a session-specific scoring rubric (Supporting File S10). Follow-up questions for this lab session include (i) an invitation for students to share two data sets that, if their similarity or dissimilarity were known, would impact their lives and (ii) a brief description of a hypothetical experiment, for which students suggest ways to reduce uncertainty (Supporting File S11).
Session 3. Distinguishing Data Sets
The third session begins with a discussion about distinguishing data sets. Instructors may choose to open by sharing student examples of data sets that matter to them or their communities (in the Lab Follow-Up Question from the previous week). Supporting File S12 also includes educational data sets distinguishing student performance in active engagement vs. traditional lecture classes, as well as data from two different methods of measuring the Hubble constant. The Hubble constant data sets are especially valuable for making the point that reducing uncertainty is essential to distinguishing data sets: early data indicated that two different methods of measuring the constant were likely in agreement, but as later experiments reduced uncertainty, it became clear that the measurements were entirely distinct.
Finally, the opening discussion introduces a measure of distinguishability that the students will know as “t-prime.” This is a generalized form of a t-value seen in statistics, adapted here for any measurement with uncertainty, not only means and standard deviations. For two data sets A and B, t-prime is the difference between the means divided by the combined uncertainties:
This quantity is new to most students but is consistent with their ideas from the previous session that distinguishability is relative to both uncertainty and to the difference of the means. Students are also introduced to a rubric for interpreting values of t-prime and taking appropriate action:
-
t’ << 1: Uncertainty is very large compared to the difference between the means. Reduce uncertainty.
-
t’ ≈ 1: Data sets are indistinguishable: data sets may represent the same phenomenon.
-
1 < t’ < 3: Gray area: data sets may or may not represent the same phenomenon. Reduce uncertainty.
-
t’ > 3: Data sets are distinguishable: data sets probably do not represent the same phenomenon.
Student teamwork focuses on quantitative comparison of data sets (Supporting File S13). After checking in on their team agreement, students calculate and interpret the t-prime value for their data sets from the previous week. Based on this quantitative measure, they reflect on the likelihood that the period of the pendulum released at 10° is distinguishable from the period of the pendulum released 20°. Students typically find that they need to reduce their uncertainty further to tell whether the data sets are distinguishable, and accordingly spend the rest of the session further improving their experiment. They continue to consult with other groups to learn about their approaches and ideas. Their lab notebooks should document at least two different attempts to reduce the uncertainty in their measurements, each with their own data and a comparison of the effectiveness of the method, including calculations of t-prime. Finally, students offer an evidence-based response to the experimental question: “Is the period of a pendulum released at 10° different from one released at 20°?”
The scoring rubric for this session includes data collection, uncertainty reduction, and comparison of data sets (Supporting File S14). The follow-up question for this session (Supporting File S15) invites students to (i) reflect on whether knowing (or thinking you know) the “correct” result of an experiment can create confirmation bias (bias in favor of confirming one’s expectations), and (ii) determine strategies that can mitigate these potential issues. This reflection opportunity prepares students to consider issues of scientific integrity, which are a focus of the next unit.
Teaching Discussion
Instructional Experience
Research demonstrates that students experiencing this kind of lab can engage in the intended scientific practices (2, 22): they can understand sources of uncertainty in measurement and the importance of reducing uncertainty, value the role of uncertainty in making comparisons between measurements, connect the activities in lab to authentic scientific practice and their everyday lives, and understand the importance of working collaboratively. Our experience is that supporting students to engage in these practices creates a highly enjoyable dynamic between students and instructors: because the experimental questions can only be answered experimentally, the students and instructors are on the same side, looking together at a phenomenon. There is an atmosphere of shared problem-solving and creative freedom: the students should do whatever they can do to answer the experimental question, within the constraints of allotted time, resources, and existing knowledge (constraints that also apply to professional scientists). Different teams obtain somewhat different findings because of their different methods and/or the variability of nature, and therefore can authentically grapple with reconciling their results, instead of “deciding who’s right.” Students experience the confirmation bias that is an inevitable part of being human and learn the scientific community’s practices for mitigating bias. Overall, the instructional atmosphere contrasts strongly with the situation in a lecture class, where the instructor “has” the knowledge and students are hoping to “get it from” them.
By observing other instructors facilitating this series of activities, we have identified ways in which instructors both succeed and struggle in responding to student confirmation bias (23). An example of a successful response is to identify students’ attempts to confirm an expected result through careful messaging, such as by reminding them that the goal is to be a scientist and explore the phenomenon, not to verify a textbook answer. Alternatively, the instructor can guide students explicitly to consider whether the period should be equal at all possible angles (e.g., “what is the period from an amplitude of zero degrees?”). On the other hand, instructor messaging that “gamifies” the lab can be problematic, such as focusing on whether they will be graded for getting a particular result.
At some of the universities at which the authors have implemented this lesson, approximately half the students “know” the pendulum formula and (on this basis) expect that the period is independent of angle. Physics majors may be more familiar with the formula and derivation than other students. “Knowing” the formula and derivation can have multiple effects. On the one hand, it allows students to critically evaluate the precision of their experiment relative to the approximation. On the other hand, it can corner students into trying to prove (or disprove) the angle dependence on the period, leading them to questionable research practices. In other university contexts, few students are aware of the pendulum formula and so are likely to experience more “discovery.”
Supporting Materials
-
S1. Quantifying Uncertainty – Lab practices scoring rubric
-
S2. Quantifying Uncertainty – Group roles handout
-
S3. Quantifying Uncertainty – Session 1: Measuring uncertainty slides
-
S4. Quantifying Uncertainty – Session 1: Measuring uncertainty instructions for students
-
S5. Quantifying Uncertainty – Statistics vocabulary reference sheet
-
S6. Quantifying Uncertainty – Session 1: Measuring uncertainty scoring rubric
-
S7. Quantifying Uncertainty – Session 1: Measuring uncertainty follow-up question
-
S8. Quantifying Uncertainty – Session 2: Reducing uncertainty slides
-
S9. Quantifying Uncertainty – Session 2: Reducing uncertainty instructions for students
-
S10. Quantifying Uncertainty – Session 2: Reducing uncertainty scoring rubric
-
S11. Quantifying Uncertainty – Session 2: Reducing uncertainty follow-up question
-
S12. Quantifying Uncertainty – Session 3: Comparing data sets slides
-
S13. Quantifying Uncertainty – Session 3: Comparing data sets instructions for students
-
S14. Quantifying Uncertainty – Session 3: Comparing data sets scoring rubric
-
S15. Quantifying Uncertainty – Session 3: Comparing data sets follow-up question
Acknowledgments
This sequence of activities is based on previous versions of the period of a pendulum lab that have been developed over the last decade. We particularly acknowledge the contributions of D. A. Bonn (for the original version of the experiment), James Day and Ido Roll (for developments of the invention activity), Emily Smith (for updated instructions and the idea for Reviewer #2), Phil Krasicky and Rebeckah Fussell (for aspects of the uncertainty and distinguishability questions). This material is based on work supported by the National Science Foundation under Grant No. 2000739.
References
- Holmes NG, Wieman CE. 2018. Introductory physics labs: We can do better. Phys Today 71:38–45. doi:10.1063/PT.3.3816.
- Holmes NG, Wieman CE, Bonn DA. 2015. Teaching critical thinking. Proc Natl Acad Sci 112:11199–11204. doi:10.1073/pnas.1505329112.
- Smith EM, Holmes NG. 2021. Best practice for instructional labs. Nat Phys 17:662–663. doi:10.1038/s41567-021-01256-6.
- Kozminski J, Lewandowski H, Beverly N, Lindaas S, Deardorff D, Reagan A, Dietz R, Tagg R, Eblen-Zayas M, Williams J, Hobbs R, Zwickl B. 2014. AAPT recommendations for the undergraduate physics laboratory curriculum. American Association of Physics Teachers, College Park, MD. https://www.aapt.org/resources/upload/labguidlinesdocument_ebendorsed_nov10.pdf.
- Holmes NG, Bonn DA. 2015. Quantitative comparisons to promote inquiry in the introductory physics lab. Phys Teach 53:352–355. doi:10.1119/1.4928350.
- Smith EM, Stein MM, Holmes NG. 2020. How expectations of confirmation influence students’ experimentation decisions in introductory labs. Phys Rev Phys Educ Res 16:010113. doi:10.1103/PhysRevPhysEducRes.16.010113.
- Smith EM, Stein MM, Walsh C, Holmes NG. 2020. Direct measurement of the impact of teaching experimentation in physics labs. Phys Rev X 10:011029. doi:10.1103/PhysRevX.10.011029.
- Barton AC, Tan E. 2010. We be burnin’! Agency, identity, and science learning. J Learn Sci 19:187–229. doi:10.1080/10508400903530044.
- Luck M, d’inverno M. 1995. A formal framework for agency and autonomy, p 254–260. Proceedings of the First International Conference on Multi-Agent Systems (ICMAS-95). ICMAS, San Francisco, CA.
- Holmes NG, Keep B, Wieman CE. 2020. Developing scientific decision making by structuring and supporting student agency. Phys Rev Phys Educ Res 16:010109. doi:10.1103/PhysRevPhysEducRes.16.010109.
- Wilcox BR, Lewandowski HJ. 2016. Open-ended versus guided laboratory activities: Impact on students’ beliefs about experimental physics. Phys Rev Phys Educ Res 12:020132. doi:10.1103/PhysRevPhysEducRes.12.020132.
- Arnold J, Clarke DJ. 2014. What is ‘agency’? Perspectives in science education research. Int J Sci Educ 36:735–754. doi:10.1080/09500693.2013.825066.
- Buck LB, Bretz SL, Towns MH. Characterizing the level of inquiry in the undergraduate laboratory. J Coll Sci Teach 38:52–58.
- Smith EM, Stein MM, Holmes NG. 2018. Surprise! Shifting students away from model-verifying frames in physics labs. In Traxler AL, Cao Y, Wolf SF (ed), 2018 Physics Education Research Conference Proceedings. AIP Publishing, College Park, MD. doi:10.1119/perc.2018.pr.Smith.
- Stein MM, Smith EM, Holmes NG. 2018. Confirming what we know: Understanding questionable research practices in intro physics labs. In Traxler AL, Cao Y, Wolf SF (ed), 2018 Physics Education Research Conference Proceedings. AIP Publishing, College Park, MD. doi:10.1119/perc.2018.pr.Stein.
- Day J, Adams W, Wieman CE, Schwartz DL, Bonn DA. 2014. Invention activities: A path to expertise. Phys Can Spec Issue Phys Educ Res 70:81–83.
- Schwartz DL, Martin T. 2004. Inventing to prepare for future learning: The hidden efficiency of encouraging original student production in statistics instruction. Cogn Instr 22:129–184. doi:10.1207/s1532690xci2202_1.
- Schwartz DL, Chase CC, Oppezzo MA, Chin DB. 2011. Practicing versus inventing with contrasting cases: The effects of telling first on learning and transfer. J Educ Psychol 103:759–775. doi:10.1037/a0025140.
- Day J, Holmes NG, Roll I, Bonn DA. 2013. Finding evidence of transfer with invention activities: Teaching the concept of weighted average, p 117–120. In Engelhardt PV, Churukian AD, Jones DL (ed), 2013 Physics Education Research Conference Proceedings. AIP Publishing, College Park, MD. doi:10.1119/perc.2013.pr.017
- Roll I, Aleven V, Koedinger K. 2011. Outcomes and mechanisms of transfer in invention activities, p 2824–2829. In Carlson L, C Hölscher C, Shipley T (ed), Proceedings of the 33rd Annual Conference of the Cognitive Science Society. Cognitive Science Society, Austin, TX.
- Etkina E, Van Heuvelen A, White-Brahmia S, Brookes DT, Gentile M, Murthy S, Rosengrant D, Warren A. 2006. Scientific abilities and their assessment. Phys Rev ST Phys Educ Res 2:020103. doi:10.1103/PhysRevSTPER.2.020103.
- Zwickl BM, Hu D, Finkelstein N, Lewandowski HJ. 2015. Model-based reasoning in the physics laboratory: Framework and initial results. Phys Rev ST Phys Educ Res 11:020113. doi:10.1103/PhysRevSTPER.11.020113.
- Sundstrom M, Fussell R, Scherr RE, Holmes NG. 2022. Students’ varying responses to instructor prompts for frame shifts in physics labs, p 451–456. In Frank BW, Jones D, Ryan QX (ed), 2022 Physics Education Research Conference Proceedings. AIP Publishing, College Park, MD. doi:10.1119/perc.2022.pr.Sundstrom.
Article Files
Login to access supporting documents
Scherr-Holmes-Quantifying Uncertainty and Distinguishing Data Sets in Introductory Physics.pdf(PDF | 249 KB)
S1. Quantifying Uncertainty - Lab practices scoring rubric.docx(DOCX | 15 KB)
S2. Quantifying Uncertainty - Group roles handout.docx(DOCX | 21 KB)
S3. Quantifying Uncertainty - Session 1 Measuring uncertainty slides.pptx(PPTX | 1 MB)
S4. Quantifying Uncertainty - Session 1 Measuring uncertainty instructions for students.docx(DOCX | 17 KB)
S5. Quantifying Uncertainty - Statistics vocabulary reference sheet.docx(DOCX | 117 KB)
S6. Quantifying Uncertainty - Session 1 Measuring uncertainty scoring rubric.docx(DOCX | 17 KB)
S7. Quantifying Uncertainty - Session 1 Measuring uncertainty follow-up question.docx(DOCX | 16 KB)
S8. Quantifying Uncertainty - Session 2 Reducing uncertainty slides.pptx(PPTX | 1 MB)
S9. Quantifying Uncertainty - Session 2 Reducing uncertainty instructions for students.docx(DOCX | 17 KB)
S10. Quantifying Uncertainty - Session 2 Reducing uncertainty scoring rubric.docx(DOCX | 16 KB)
S11. Quantifying Uncertainty - Session 2 Reducing uncertainty follow-up question.docx(DOCX | 17 KB)
S12. Quantifying Uncertainty - Session 3 Comparing data sets slides.pptx(PPTX | 261 KB)
S13. Quantifying Uncertainty - Session 3 Comparing data sets instructions for students.docx(DOCX | 18 KB)
S14. Quantifying Uncertainty - Session 3 Comparing data sets scoring rubric.docx(DOCX | 16 KB)
S15. Quantifying Uncertainty - Session 3 Comparing data sets follow-up question.docx(DOCX | 14 KB)
- License terms

Comments
Comments
There are no comments on this resource.